幻影彭的彩虹

记录青春的扇区

0%

Tarjan算法和坑

发表于 分类于 ，

Tarjan算法和坑

某场多校，某道题，有负环，需要排除（负环）。

某人写了，又交了，吃罚时，需要排除（某人）。

队友写了，又交了，他过了，某人完了。

数据有了，调试了，调完了，Tarjan锅了。

本文提一下 Tarjan 算法里的坑。

算法流程和原理

通过对图进行 DFS 遍历，得到 DFS 树。

容易发现每个 SCC 是一个树上的联通块，这是由 DFS 的过程保证的，如果分开了，那么就不满足 DFS 的性质。

DFS 一个点，会访问到所有它能到的点。由于它们是 SCC，所以 DFS 该 SCC 的任意节点的时候，一定会让 SCC 中所有未访问的节点都在它的子树里，所以不会出现断开的情况。

考虑树的每个节点是否为 SCC 的根。定义一个节点为 SCC 的根，当且仅当这个节点是该 SCC 中最浅的节点。

定义 low[u] 为 $u$ 能通过自己或者自己的子树到达的点，时间戳的最小值。维护一个栈，表示当前还没有确定连通块的节点。

如果一个点 $u$ 的 low[u]=dfn[u]，那么该点无法到达时间戳更小的点，所以一定是 SCC 的根，弹出所有栈中的值直到 $u$，作为该 SCC 的所有点。

如果访问了一个已经访问过的点 $v$，分两种 CASE，其一是它已经被弹栈了，这样的话该边一定是横插边，直接不管，因为 $v$ 到不了 $u$。如果还没有弹栈，说明该点的 SCC 还没有确定，所以这个点是可以到 $u$ 的父亲的，也能到 $v$。所以这种点是有效的，$u$ 因此能到达更上面的点，不是 SCC 的根。

不同的写法

省略全局变量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//AC Code
void dfs(int u){
	dfn[u]=low[u]=++s;
	st[++top]=u;in[u]=1;
	for(int i=0;i<e[2][u].size();i++){
		int v=e[2][u][i].v,w=e[2][u][i].e,f=e[2][u][i].f;
		if(dfn[v]){
			if(in[v])cmin(low[u],dfn[v]);
			continue;
		}
		dfs(v);cmin(low[u],low[v]);
	}
	if(dfn[u]==low[u]){
		cnt++;int v;
		do rk[v=st[top--]]=cnt,in[v]=0; while(v!=u);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//AC code
void dfs(int u){
	dfn[u]=low[u]=++s;st[++top]=u;
	for(int i=0;i<e[2][u].size();i++){
		int v=e[2][u][i].v,w=e[2][u][i].e,f=e[2][u][i].f;
		if(dfn[v]){
			if(!rk[v])cmin(low[u],dfn[v]);
			continue;
		}
		dfs(v);cmin(low[u],low[v]);
	}
	if(dfn[u]==low[u]){
		cnt++;int v;
		do rk[v=st[top--]]=cnt; while(v!=u);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//WA code
void dfs(int u){
	dfn[u]=low[u]=++s;st[++top]=u;in[u]=1;
	for(int i=0;i<e[2][u].size();i++){
		int v=e[2][u][i].v,w=e[2][u][i].e,f=e[2][u][i].f;
		if(dfn[v]){
			if(in[v])cmin(low[u],dfn[v]);
			continue;
		}
		dfs(v);cmin(low[u],low[v]);
	}
	if(dfn[u]==low[u]){
		cnt++;int v;
		do rk[v=st[top--]]=cnt; while(v!=u);
	}
	in[u]=0;
}

注意到前两种 Code 维护的都是栈中元素，因此没有问题。

但第三种写法，维护的是所有的祖先，当当前节点 $u$ 连接到的点 $v$，可以通过其返祖边回到更上面的父亲时，这种做法会漏掉 $v$。因此是错误的。

举个例子。

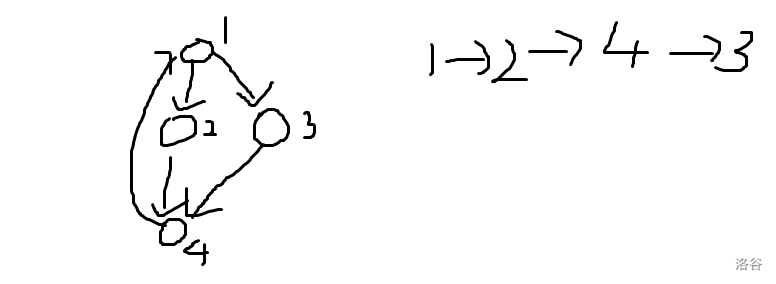
访问 $3$ 时，$4$ 已经从 $in$ 中移除，但是我们仍然可以通过 $4$ 到达 $3$，所以会出现错误。

洛谷的模板题，数据相当之水，第三种做法可以通过，但它是错误的。

一些碎碎念

缩点的时候，也就是求强连通分量，$low[u]$ 和 $low[v],dfn[v]$ 取 min，都是可以的，因为不影响判断某个点是否是 SCC 的根。

如果图是无向图，那么不会存在横插边的问题，所有边都是返祖边。

求边双连通分量，和 low[v] 取 min 同样没有问题，因为不影响一个点是不是边双的根的判断。

判断一个点是边双根的方式是，它无法通过自己或者儿子，到达更上面的点。这也意味着，该点与其父亲的连边是桥。

边双连通具有传递性

求点双连通分量，判断割点，如果和 low[u] 取 min，是会出问题的。

判断一个点是割点的方式是，它的任意一个儿子无法在没有它的情况下到达上面的点。特别注意，该点如果没有儿子，就不是割点。

点双，就是以割点为界的所有连通块。

下图是一个取 low[v] 出问题的例子。

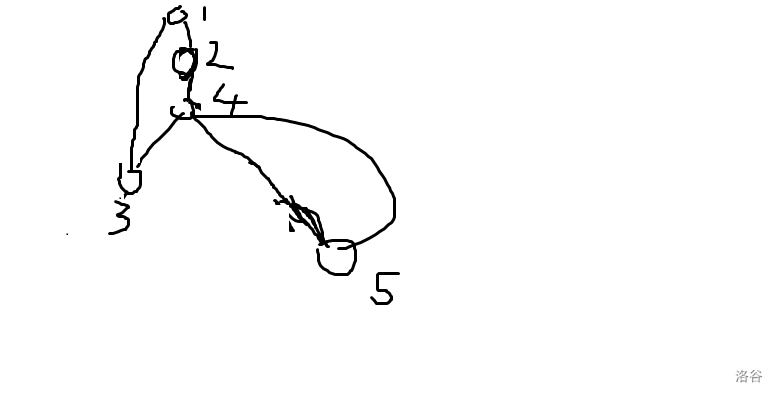
先访问 $3$，再访问 $5$，会错误的认为 $5$ 能够到 $1$，我们 low 的定义是通过自身或自身的子树能到的最小时间戳，而如果和 low[v] 取 min，就势必会经过其它的点。在这里，$5$ 通过了 $4$ 到达 $1$，因此如果删去 $4$，$5$ 就不能到 $1$，这里需要保证定义的严谨性。

前面的强连通分量，只需要能够到达，但不关心怎么到达，所以没问题。

边双也只关心能否到达更前面点，所以没有问题。