QQ 群一笔画问题
Author:Huan_yp
一笔画问题,即给定一张无向图 $G(V,E)$,每个点的度数均为偶数或者仅有两个点度数为奇数,需要求出一条不重复经过边的路径,遍历所有的边。
由于在算法竞赛中,这个问题是简单的,这里只讨论在 QQ 群一笔画中,快速解决问题的方式。
归纳构造法证明
已知给定图为一笔画图,故一定满足每个点的度数均为偶数或者仅有两个点度数为奇数,并且图联通,若存在两个点度数为奇数,则从其中一个点开始,否则可以从任意点开始。
执行以下过程。
- 在当前节点任意找一条边,如果可以找到,则重复此过程。
- 如果无法找到:
- 图已经被遍历,结束,得到保存的路径。
- 该点度数为 $0$,所以一定回到了起点或者到了终点。记录并删除该路径中所有边,并回溯到上一个存在出度的点,可以证明一定存在这样的点,否则图不连通。该点的度数一定为偶数,对该点进行上述过程,得到一条首尾相接的路径,插入到原路径,得到完整的欧拉(回)路。
- 容易发现,这样的过程将图遍历了一遍,所以最后得到的是完整的欧拉路径。
代码实现比较简单,只需要使用栈在退出时记录当前节点,得到的,从栈顶到栈底,就是一条完整的欧拉路径。
下面是一个例子:
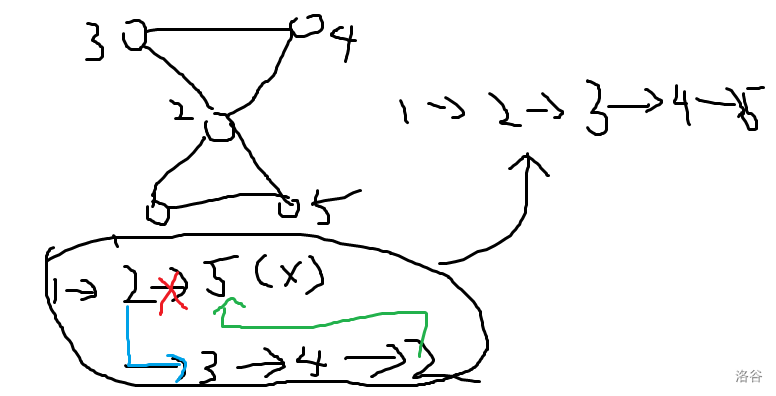
按 $1->2->5$ 走,$5$ 处无路可走,回到 $2$,记录一条路径 $2->5$,从 $2$ 继续走 $2->3->4->2$,回到了,插入原路径变为 $1->2->3->4->2->5$。
正确的操作方式
由于找边的耗时比较长,我们需要尽可能少的找边。
- 如果有 API 可以读取边的情况,那么直接做一遍上述过程即可得到答案。
- 如果不存在对应的 API,我们直接进行上诉操作,可以拿一个程序记录已经走过的点和边并提示路径。
- 如果图不为欧拉回路,则存在死路,判断方式比较简单,当前点是否为起始点,如果死路位于起始点,直接进行路径回溯操作,即步骤二。否则撤销所有操作,从当前节点开始逆向进行已经进行过的操作。
这样单纯的找边的次数恰好为 m 次,即边数。
回溯和走边的操作总和不会超过 2m。
平均执行次数
考虑图为随机生成,期望的行走次数,感觉是 polylog 级别,但是我不会证明。
蒙特卡洛模拟
咕咕咕,没时间写代码。
采用蒙特卡洛模拟算法对该结论进行验证
严谨数学证明
咕咕咕。
也许可以考虑每条边回溯次数期望 $e_{u,v}$。