幻影彭的彩虹

记录青春的扇区

0%

洛谷P6025题解

发表于 更新于

洛谷P6025 题解

提供一个复杂度为的 $O(\log n)$ 的，基于正常分析而非打表的做法，我认为这个做法比当前题解区的所有做法更加优美。

这道题相当不错，考察了线段树和位运算的理解。

题意

  • 一颗常规方式构建的线段树，求大小为 $1,2,3,\cdots n$ 的线段树分别占用的最大空间，即最大下标。

  • 输出答案的异或和。

  • $n\leq 10^{15}$

构建代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void build(int k,int l,int r)
{
	if(l==r)
	{
		//do something
		//e.g. tree[k]=a[l]
		return;
	}
	int mid=(l+r)>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
	//do something
	//e.g. tree[k]=tree[k<<1]+tree[k<<1|1]
}

原题意是求 $f(l,r)$，但很容易转化为求 $f(1,n)$，直接求 $f(1,l-1)\bigoplus f(1,r)$ 即可。

分析

40PTS

首先，线段树建立的过程，就是从根往下走的过程，往左走，向当前编号的二进制表示后写一个 $0$，往右走，就写一个 $1$。

考虑线段树的最大下标在何处取到，由于右儿子下标相对较大，一个比较显然的想法是一直走右儿子，但是这样是错误的，显然的反例为 $n=3$，如下图所示。

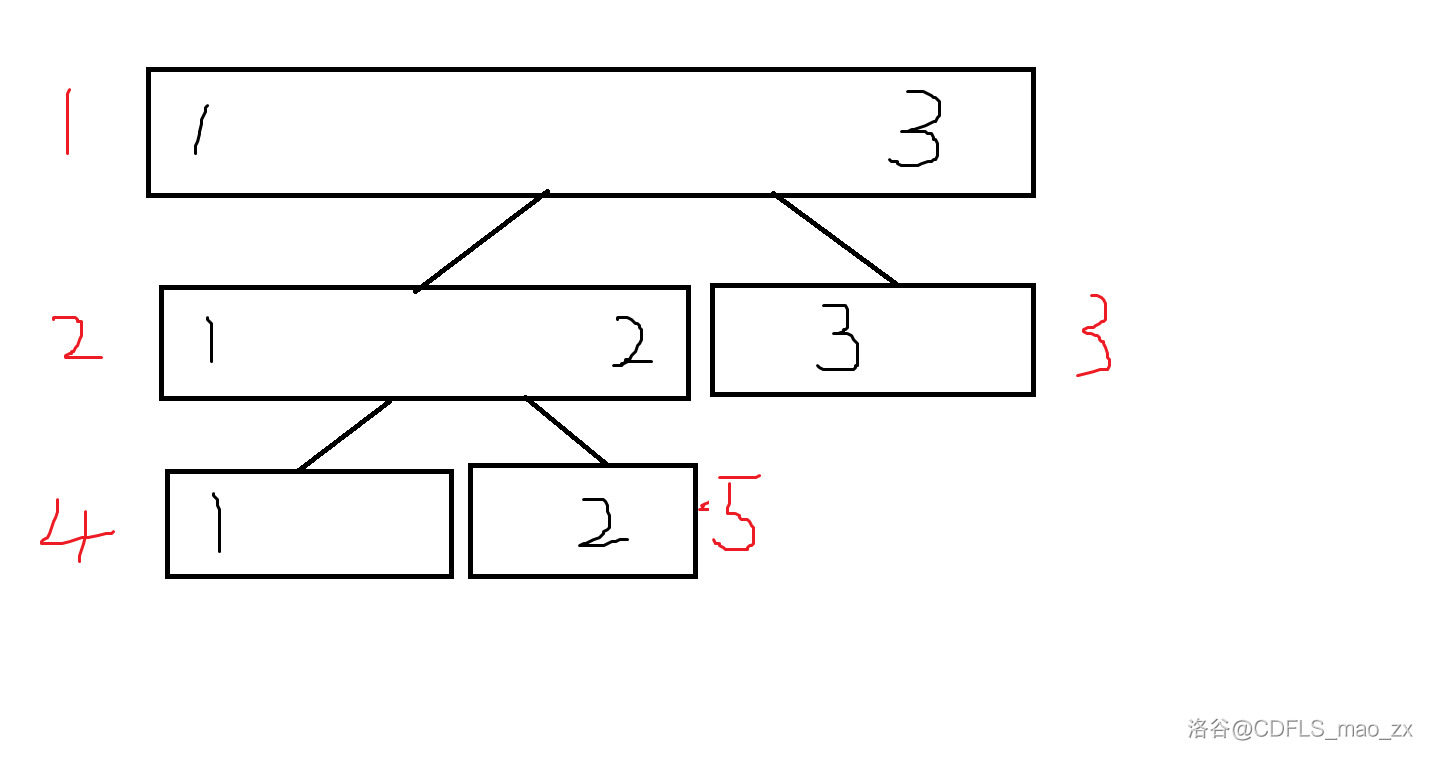
这个例子中，$[1,3]$ 节点的左儿子比右儿子多一层，所以出现了走左儿子最优的情况。

但是，如果某个节点处左右儿子高度相同，那么很显然应该走右儿子，因为当前这一步决定的位数是最高位。

所以走左儿子，当且仅当左右儿子高度不同，下面分析线段树的高度和长度的关系。

首先，子树构建情况只和长度有关，所以我们只关心长度而非左右端点，然后，长度为 $2^k$ 的节点，构建出的树为一颗完全二叉树，其高度为 $k$。 此时，如果点数继续增大，那么高度为 $k$ 的树就无法容下这么多节点，高度会变为 $k+1$，所以，长度为 $(2^k,2^{k+1}]$ 的节点，构建出子树的高度为 ${k+1}$。

容易发现，常规构建方式构建出的子树，其左儿子的大小不小于右儿子，且差值至多为 1，因此，如果出现了左右儿子高度不同，一定是左儿子比右儿子高，并且只能是一种情况，即长度的二进制表示为 $100001$。即除了最高位和最低位其余位均为 $0$，只有这样才会出现左右儿子落在不同区间的情况。

所以我们对于一个 $n$，很容易给出一个 $O(\log n)$ 的计算方式，即：

1
2
3
4
5
int ask(int x,int now=1){
	if(x==1)return now;
	if(__builtin_popcount(x)==2&&x&1)return ask(x+1>>1,now*2);
	return ask(x>>1,now*2+1);	
}

其中 __builtin_popcount() 为内置函数，参数为 unsigned， int 也可以使用但不能为负数。

如果希望对 long long 使用，应改为 _builtin_popcountll()。

对每个数暴力求解即可。

100PTS

我们需要观察求解一个数的过程，不妨考虑二进制数 $1001011$ 的计算过程。

手动模拟一下上述 $\operatorname{ask()}$ 函数的调用过程，$now$ 变量和 $x$ 变量的值依次变为 

1
2
3
4
5
6
7
8
now=00000001 x=1001011
now=00000011 x=0100101
now=00000111 x=0010010
now=00001111 x=0001001
now=00011110 x=0000101
now=00111100 x=0000011
now=01111000 x=0000010
now=11110001 x=0000001

容易发现，在出现 $1001$ 这样的情况之前，我们将 $now$ 左移一位并在后面写上了 $1$，同时将 $x$ 右移一位。

在出现 $1001$ 之后，我们一直在往 $now$ 后面写 $0$，而 $x$ 的变化则是先右移一位并将最后一位改为 $1$。

而最后 $x$ 从 $10$ 变为 $1$ 时，我们在 $now$ 末尾添加了一个 $1$。

不难发现，一个固定的 $x$，我们最终得到的占用下标最大值，仅仅和它二进制表示下的最高位和第二高的为 $1$ 的位有关，因为在这之前我们一定会添加 $1$，而在这之后一定会往后添加 $0$ 并在最后添加一个 $1$。

注意如果为 $2^k$ 这样不存在次高位的数，我们需要特判。

所以我们有了一个比较显然的想法，即枚举二进制下最高位和次高位的位置，统计能取到这两个位置的数的数量，并异或上对应的权值。

这样的复杂度是 $O(\log^2n)$ 的，我们考虑继续优化。

对于二进制下位数小于 $n$ 的二进制下位数的所有数，实际上会有贡献的只有两个值，分别是 $2^k$ 和 $2^k+1$。因为如果次高位不为第一位，那么能取到该值的数的个数一定为偶数个（低于次高位的位置可以任意填）。剩下这两个值的贡献都是可以 $O(1)$ 计算的。

这样就只用考虑二进制下位数和 $n$ 相同的数，同样的道理，如果次高位高于 $1$，那么没有贡献，但需要注意的是，如果次高位取到了上界，例如 $10110$ 中，次高位取到了第三位的 $1$，那么由于必须小于 $n$，实际上只有奇数个值可以取到，这样会带来一定的贡献，所以我们需要计算这种情况的答案，复杂度为 $O(\log n)$。

总复杂度$O(\log n)$。

可以参考我博客中的一些线段树的总结，会不定期更新。

从ZKW线段树看线段树的性质

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<bits/stdc++.h>
#define y1 y3647
#define int long long
#define pii pair<int,int>
#define low(x) ((x)&-(x))
using namespace std;
template<typename _type>
inline void read(_type &x){
	x=0;int f=1;char ch=getchar();
	while(ch!=45&&(ch>'9'||ch<'0'))ch=getchar();
	if(ch==45){f=-1,ch=getchar();}
	while(ch<='9'&&ch>='0'){x=x*10+ch-48;ch=getchar();}x*=f;
}
template<typename _type1,typename _type2>void cmin(_type1 &a,const _type2 b){if(a>b)a=b;}
template<typename _type1,typename _type2>void cmax(_type1 &a,const _type2 b){if(a<b)a=b;} 
int i,j,k,n,s,t,m,tp1,tp2;
int solve(int x){
	if(x==0)return 0;
	if(x==1)return 1;
    //特判边界情况
	int res=1,h=log2(x);
    //最高位从 10 开始枚举,所以 res 初值应该设置为 1
    //h 为二进制下 x 的位数
	for(i=1;i<h;i++){
		res^=(1ll<<i+1)-1;
		res^=(1ll<<i+1)+1;
        //注意左移操作的 1 是 long long 级别的数
        //计算 2^k 和 2^k+1 的答案,其它位置没有贡献 
	}
	res^=(1ll<<h+1)-1;
    //计算 2^h 的答案
	if(low(x)==x)return res;
    //如果 x=2^h,无需进行下面的步骤
	res^=(1ll<<h+1)+1;
	if(x-1==1ll<<h||x&1)return res;
    //如果 x=2^h+1 或者末尾为 1,那么之后取到的值个数一定是偶数,无需计算。
	int now=1;
	while(__builtin_popcountll(x)>2||(x&1)==0){
		now=now<<1|1;
		x>>=1;
	}
    //模拟求解的第一步,找到对应的次高位,在这之前往后写 1
	while(x){
		x>>=1;
		now<<=1;
	}
    //模拟求解第二步,往后写 0
	now|=1;
    //记得左右还需要异或 1
	return res^now;
}
signed main()
{
// 	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
//	freopen(".in","w",stdout);
	int l,r;
	read(l),read(r);
	printf("%lld\n",solve(r)^solve(l-1));
	return 0;
}