计算几何
写一下学计算几何的感悟。
向量
点积
$\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}|\times|\mathbf{b}| \times \cos\theta = x_1x_2+y_1y_2$
常用来计算向量夹角。
叉积
$\mathbf{a} \times \mathbf{b} = |\mathbf{a}|\times |\mathbf{b}|\times \sin\theta = x_1y_2-x_2y_1$
几何意义是两个向量围成的平行四边形的面积。
从 $\mathbf{a}$ 旋转到 $\mathbf{b}$,如果角度小于 $\pi$,那么为正,否则为负。
证明的话,方向是直接定义的,先不管,尝试证明。
我觉得这个不太适合用 markdown 写下来。
为什么方向是对的,可以替换一下 $x,y$ 变成 $\sin,\cos$,然后很自然是对的。
可以用来求线段交点。
算一下 $BCD,ACD$ 的面积,用相似求 $AO$,就可以得到 $O$ 点坐标。
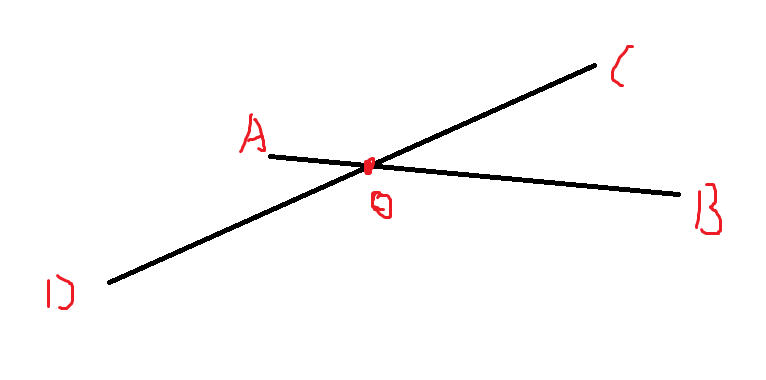
向量旋转
有人不会用这个东西,我不说是谁。
$\mathbf{a}$ 转 $\alpha$ 角:$(|\mathbf{a}|\cos(\theta+\alpha),|\mathbf{a}|\sin(\theta+\alpha))$。
和差角公式记不住的话朱某要来找麻烦,所以有人还是能记住。
多边形
三角剖分
$S=\dfrac{\sum\mathbf{a_i}\times \mathbf{a_{(i+1)\%n}}}{2}$
盗一波图。
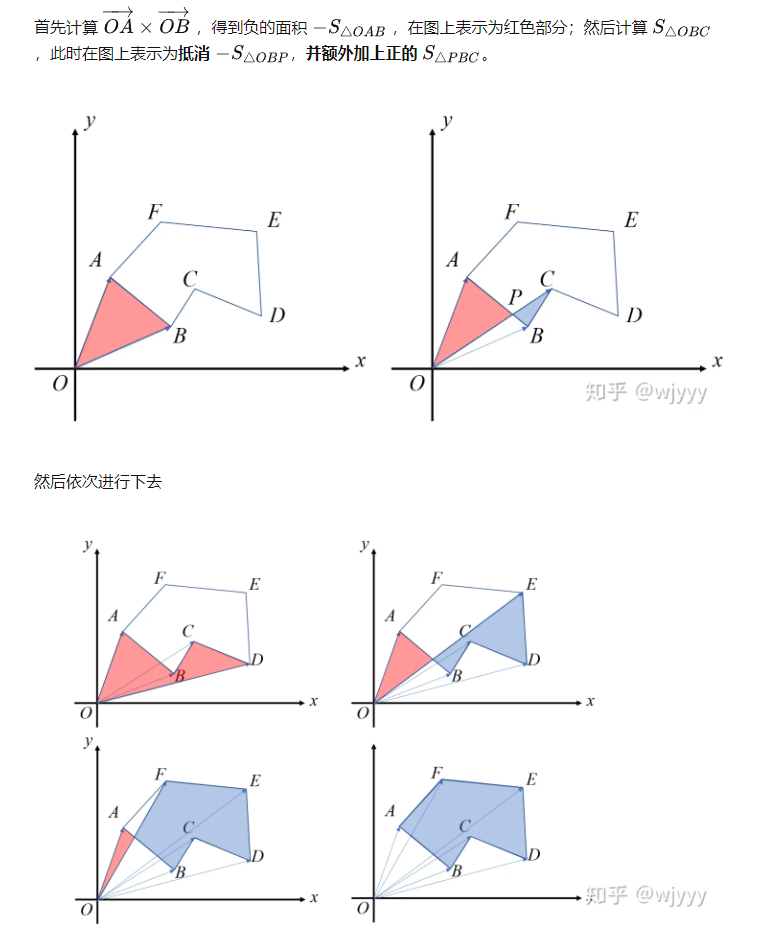
凸包
按照逆时针方向看,多边形凸包永远往左拐。
直线
可以用一个点 $P$ 加方向向量 $\mathbf{v}$ 存储,也可以顺便记一个 $P_2$。
点在直线的哪边
求 $PQ\times \mathbf{v}$ 即可,为正在下方,为负在上方,$0$ 则在线上,前提条件是向量 $\mathbf{v}$ 的 $x$ 为正 。
快速排斥实验和跨立实验
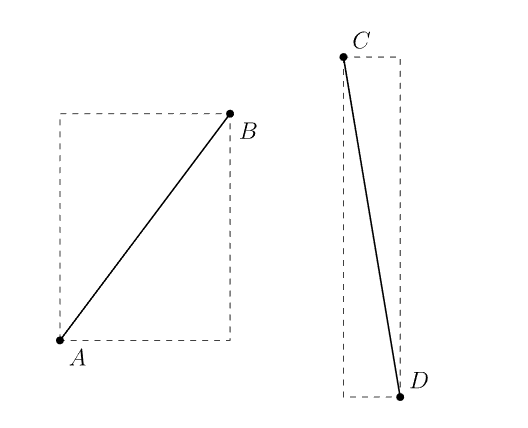
两个矩阵不交,则通过快速排斥实验。
比较简易的方式是对于两维独立判断线段是否有交,如果任何一维无交,则通过快速排斥实验。
跨立实验则是判断一条线段的两端是否在另一条线段的两边,可以用向量叉乘做。
相互做跨立实验,如果均能通过,则线段有交或共线,结合快速排斥实验可以判断线段是否有交。
两条线段共线但不交也能通过跨立实验。
两直线交点
先判断平行和重合。
然后对于两条直线 $(P_1,\mathbf{a_1}),(P_2,\mathbf{a_2})$,设 $Q=k\mathbf{a_1}+P_1$,则有 $(P_2-(k\mathbf{a_1}+P_1))\times \mathbf{a_2}=0$
叉积有分配律,所以直接拆开解 $k$ 然后带回去。
$k=\dfrac{(P_2-P_1)\times \mathbf{a_2}}{\mathbf{a_1}\times\mathbf{a_2}}$
如果你敢约分,朱某就敢把你鲨了。
线和直线的垂足
算出 $PQ$ 在 $\mathbf{v}$ 上投影的长度和方向(点积),$P$ 加上这个就行。
点到直线距离
可以先算垂足,也可以用记下来的另一个点带面积公式算。
角平分线
模长相同的方向向量相加,得到角平分线的方向向量,证明考虑构造菱形。
凸包
于是乎求凸包的时候多了一种判定方式:
如果是上凸包,弹出点的充要条件是上个点在该点与上上个点的连线下方
下凸包,弹出条件就是在上方,比斜率好一点,而且判共线很方便。
圆
线援交圆交
求出点到直线距离和垂足,然后勾股定理算两个点。
圆圆交
半径相等可以求中点勾股定理偷懒,半径不等可以选一个三角形解三角形。
具体的,可以算出一个角的 $\cos$ 然后旋转向量,最后乘半径再加上去。
切点
勾股定理,旋转,解三角形。