ARC155
A
考虑 $k\le 2n$ 的情况,可以模拟,具体的,正着做一遍,填上对应的数字,反着做一遍,也填上对应的数字,如果合法,那么就是可以的。
考虑 $k> 2n$ 的情况,容易发现等价于 $k\bmod 4n$ 的情况,画个图:
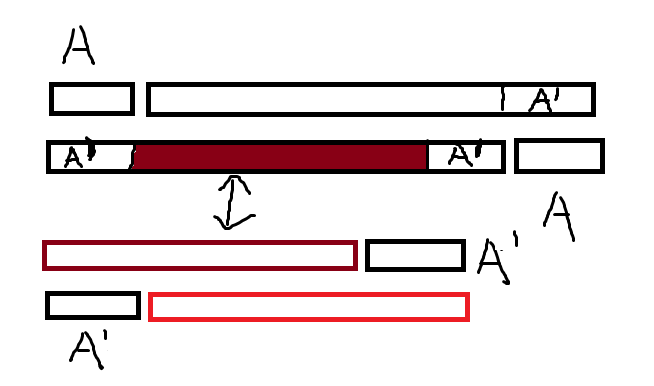
红色部分,如果满足下面的两个串都是回文,那么上面的两个串自然都是回文。
实际上循环节是 $2n$,记 $T’$ 表示 $T$ 的翻转,即令 $T’_i=T_{len-i+1}\cdots$,考虑如果 $TS$ 是回文,那么 $S’T’$ 自然也是回文,所以如果把下图的 $A’$ 换为 $A$,构造出满足条件的长度为 $k-2n$ 的串 $T$,将 $T’$ 带入进上面即可满足条件。
显然这种构造是充要的。
B
考虑式子 $||x-a|-b|$,取到最小值 $0$ 的点为 $a+b$ 和 $a-b$,考虑一个询问在一个点对上的答案,就是该区间的点到 $a+b$ 和 $a-b$ 距离的最小值,在多个点对上的答案就是到所有 $a_i+b_i$ 或者 $a_i-b_i$ 的最小值,维护一个 set 表示所有点,询问 lower_bound 即可。
C
变换问题,一般考虑找不变量。
操作可逆的变换问题,还可以考虑将两个序列同时向一个序列改变。
一般这种变换构造问题的思路是找不变量,但此题的不变量不容易找。
首先的必要条件是 $A$ 是 $B$ 的一个排列,以下讨论均认为 $A$ 是 $B$ 的排列。
注意到操作是可逆的,考虑将 $A,B$ 同时变成一个串。如果 A 可以变成一个串,但 B 不能,则 A,B 不能变成同一个串。
考虑一个串 $A$,如果 $A$ 中的任何奇数都无法移动,但 $B$ 可以,那么显然是不行的,反之亦然。考虑如果 $A,B$ 中的奇数都不能移动,那么以奇数为分割线,每个部分都要对应相同,对于长度大于 $3$ 的偶数连续段,以可重集的形式相等,对于其它段,则以序列的形式相等。
如果 $A$ 中的奇数可以移动,那么我们考虑将奇数全部移动到序列最前面。找到可以移动的两个奇数,将它们放在一起然后一直向后移动,如果碰到偶数可以直接移动,碰到奇数则移动这段奇数中最靠后的两个,直到这段奇数后没有奇数为止,然后考虑将这段奇数前的第一个偶数移动到这段奇数后面,如此操作,就可以将奇数全部放在最前面。
不少于三个偶数段可以任意交换,如果只有两个偶数,那么它们的顺序不能改变。
考虑对前面的奇数部分进行排序,将一个偶数移动到两个奇数之间,然后我们可以交换它们之后再将偶数移动回去,因此前面的奇数可以任意排序。
所以对于 $A,B$ 中都存在可以移动的两个奇数的情况,如果偶数个数不为 $2$,答案一定为 Yes,否则如果出现顺序相同,为 Yes,顺序不同为 No。
D
高维前缀和
考虑这样一个问题,给定一个序列 $a,a_i\in[1,n]$,对于 $i\in[1,n]$,计算 $a_i$ 中 $i$ 的倍数的个数 $b_i$
一种 $n\ln n$ 的做法是先算一个 $cnt_i$ 表示 $i$ 的个数,然后统计每个数 $i$ 的倍数。
另一种方式是考虑高维前缀和,记 $cnt_i$ 表示考虑到当且为止,$i$ 倍数的个数,以任意顺序枚举 $n$ 以内的质数 $p_k$,从大到小的令 $cnt_i=cnt_i+cnt_{ik}$。
复杂度是 $n\log\log n$ 的。
为什么这样是对的,考虑将 $i$ 视作一个 $n$ 维的向量,每一维表示对应质数的指数,然后就是对每一维各自先做前缀和加起来。
解法一
考虑当前选好了一个数 $A$,所有的数已经可以被分为至多 $2^6$ 类。
因为 $2357111317=510510>2\times10^5$。
首先我们只关心具体有哪些质数而不关心质数的指数。
之后的选择一定会是在一个 DAG 上走,这个 DAG 的边数是 $3^6$ 的。
考虑当前在 DAG 上的某个点,先手该如何决策,当前的数为 $A$,那么所有可以选的数被分为 $A$ 的倍数,和非 $A$ 的倍数,选非 $A$ 的倍数一定会走到下一个点。
考虑到某个点后它的倍数的个数,等于所有它的倍数减去之前用掉的数的个数,注意我们在一个点处只关心其奇偶性,所以只需要记录一维 $0/1$ 表示之前用掉了奇数个还是偶数个。
转移需要考虑同层转移和不同层转移,对于同层转移,先手当且仅当目前剩余奇数个的时候可以选择让后手走下一步。对于不同层转移,则只需要确定具体能转移到哪些点。
确定能转移到哪些点可以暴力,细节还是有点多。
改进解法
其实我们不需要这个 DAG,容易发现如果当前的 G 和用掉的数的个数就可以表达所有信息了,可以省掉建立 DAG 的步骤,同样的方式考虑 G 的同层转移和非同层转移。
对于非同层转移需要计算可以转移到哪些数字,记 $f_{g,d}$ 表示满足 $\gcd(g,A_i)=d$ 的 $A_i$ 的个数,确定 $g$ 之后从大到小枚举 $d$,计算出 $d$ 倍数的个数,然后减掉所有 $f_{g,kd}$。
易知 $g=ckd$。
复杂度考虑每个 $d$,每个 $d$ 的复杂度为 $\frac{M}{d}\ln{\frac{M}{d}}$。