幻影彭的彩虹

C 使用 malloc() 和 free() 来动态分配和释放内存，C++ 使用 new 和 delete 来动态分配和释放内存。

C 管理数据的方式

malloc && free

malloc 的时候，会在堆上分配一块内存，然后返回一个指向这块内存第一个位置的指针。同时会记录一个 metadata，存储数据大小和分配状态等信息。

malloc 分配内存初值是随机的，需要手动初始化。

当使用 free 释放内存时，会检查 metadata，根据 metadata 决定所要释放数据的大小。

metadata 的存储位置一般在首地址之前，因此 free 的时候必须 free 首地址。

结构化数据

用 struct 之类的结构体来管理数据时，指针类型直接指示了应该如何处理内存中的数据。

C++ 管理数据的方式

new && delete

直接 new 一个数据类型，比如 new int，不会设置 metadata，而是直接使用指针类型来管理内存大小，并根据指针类型调用对应构造函数来初始化数据。

new 的数据必须通过 delete 来删除，并且必须显式指定指针类型，因为 delete 不仅需要指针类型指示的内存大小，还会调用对应析构函数来释放内存。

new [] && delete []

new [] 会分配一块连续的内存，然后返回一个指向这块内存第一个位置的指针。同时会记录一个 metadata，存储数据大小和分配状态等信息。new [] 分配时会调用对应构造函数来初始化数据。

delete [] 会检查 metadata，根据 metadata 决定所要释放数据的大小。delete [] 会调用对应析构函数来释放内存。

软件级是相对于程序级的概念，软件级应用往往包含多目录多文件的大量源代码，有复杂的第三方库依赖关系。

软件级应用的编译用时往往较长，并且过程相对繁琐。

我们这里介绍使用 MinGW 系列工具和 CMake 编译 cpp 软件级应用的过程和知识。

各种文件

CMakeLists.txt

CMakeLists.txt 一般用于跨平台的大型软件级项目，用于指示 CMake 生成平台对应的编译选项，也就是 Makefile 文件。

Makefile

Makefile 文件指定 make 工具编译生成 include/，lib/，bin/ 等成品的方式，我安装的是 MinGW套件，命令是 mingw32-make。

.dll/.so

这两个是动态链接文件，.dll 是 Windows 下的，.so 是 Linux 下的。

MinGW 默认是动态链接的，编译生成的 .exe 如果找不到 .dll 就运行不了。

.dll 或者 .so 默认只会在系统路径和工作目录两个地方去找

.o

.o 是可重定向目标文件，是汇编过程生成的源文件机器语言代码。

.a

.a 是静态链接归档文件，如果采用静态链接的方式编译，就需要在编译时加上这个。

它等价于把若干个 .o 打包在了一起。

C++ 编译速通

编译步骤：

1. 预处理：把 #include 的东西全部粘贴到对应的位置，由 .cc，.cpp 生成 .i，.ii 预处理文件。
2. 编译：编译器用 C/CPP 代码生成汇编代码，由 .i，.ii 生成 .s 汇编文件。
3. 汇编：由汇编器将汇编代码编程二进制代码，由 .s 生成 .o 目标文件。
4. 链接：由链接器把汇编的机器代码 .o，打包的静态链接库 .a，动态链接库 .

静态链接和动态链接的区别：

• 静态链接在编译时便将中的实现放入了 .exe 文件，在运行 .exe 时就将代码放入内存。
• 动态链接在运行时才去 .dll 中查找实现，并在调用对应函数时将这部分代码放入内存。

无论是静态链接还是动态链接，编译时都需要指定链接库。静态和动态的区别在于将对应代码加入内存的时间。

实现通常写在 .cpp 文件中，定义通常写在 .h 文件中，#include 时一般只会 #include .h 文件，所以如果编译时不指定链接库，链接步骤就会报 Undefined Refference 错误。

GNU-make 工具的使用

类 UNIX 环境下它叫 make，但是我们用的 MinGW，反正我这里叫 mingw32-make，路径是 path/to/mingw64/bin/mingw32-make.exe ，使用时记得加环境变量。

make 和 Makefile 结合，执行一些特定的命令，完成项目的编译，避免手敲 gcc 命令。

命令格式：

1

[mingw32-]make [<目标>] <可选参数...>

常用可选参数：

• -n：不执行，只打印要执行的命令。
• -f：指定 Makefile 的路径，默认情况下 Makefile 的（相对）路径为 Makefile 或 makefile。
• -j[<num>]：多线程编译，例如 -j4 表示四线程编译。

目标是指 make 要执行的具体任务，如果没有指定目标，那么会执行第一个非伪目标。

Makefile 解读

一般情况下需要我们写 makefile 的机会不是很多，会读和改就可以了。

变量操作

• <VAR_NAME> ?= <EXPR> 条件赋值，如果还没定义这个变量才赋值，规则同递归赋值。
• <VAR_NAME> = <EXPR 递归赋值计算，每次使用时重新计算。
• <VAR_NAME> := <EXPR 立即赋值计算，只计算一次。
• $(<VAR_NAME>)：引用变量。

目标

目标的格式是 <target>:[<dependencies>]。

当 make 执行某个目标时，会对依赖项进行检查，如果依赖项对应的文件不存在，则会将先执行依赖的名字对应的目标。

例如：

1
2
3
4
5

foo: foo.o
	gcc -o foo foo.o
foo.o: foo.c
	gcc -c foo.o foo.c
	echo "compiled foo.o"

执行 make 时，过程如下：

1. 没有指定目标，会找到第一个目标 foo 执行。

2. 查找其依赖 foo.o，发现不存在，于是查找目标 foo.o。

3. 找到 foo.o 其依赖 foo.c 作为一个文件存在，于是执行 gcc -c foo.o foo.c 编译生成 foo.o。

4. 返回 2. 中步骤，依赖 foo.o 已经存在，执行 gcc -o foo foo.o 生成 foo[.exe]。

目标规则

有时候可能有很多文件，某些文件的生成方式，例如 .o，是一致的，这时可以利用目标规则来定义目标。

查找目标时，规则优先级为：越具体越优先。

目标规则大致分为三种：

1. 显式目标规则

   见上。

2. 显示模式规则

   显式模式规则使用通配符 % 来匹配任意字符，包括目录分隔符。其余同上。

   下面的 $< 和 $@ 是自动变量，下面的部分有详细解释。

   1 2 3

   %.o: %.c echo "Using generic rule" gcc -c $< -o $@

3. 隐式模式规则

   隐式规则模式用于指定生成对应后缀名的文件，常见的有：

   • .c.o: 从 .c 文件生成 .o 文件。
   • .cpp.o: 从 .cpp 文件生成 .o 文件。
   • .cpp.exe: 从 .cpp 文件申城 .exe 文件。

伪目标

一般情况下，目标会作为一个文件，通过判断文件是否已经生成来判断是否已经完成该目标。

但是，如果修改了 .cpp 源代码，但是 makefile 中有生成 .o 的过程，.o 还被保留了，那么再次 make 的时候检测到 .o 已经存在，只会用已经存在的 .o 重新链接生成一次可执行文件，没有达到重新编译的效果。所以，往往需要定义一个"清理操作"，来清理相关的文件以便重新完整编译。

"清理操作" 显然不生成文件，为了完成这个操作，引入了 "伪目标" 概念，伪目标在文件开头用 .PHONY 声明，例如：

1
2
3
4
5
6
7

.PHONY: clean
all: clean foo.o
  g++ -o foo foo.o
foo.o: foo.c
  g+++ -c foo.o foo.c
clean:
  rm *.o

这样便可以在每次执行 make 时清理缓存的 .o 文件达到重新编译的效果。

提醒：

• 伪目标表示一个过程，作为依赖时一定会被执行，如果执行返回代码为 0 才判定为完成，否则判定为没有完成，可能报错。
• 严格来说 all 也应该被定义为伪目标，实际上由于不会生成 all 文件，也就无所谓，clean 有时候不会被声明为伪目标。
• make 不指定目标时，如果存在非伪目标，那么执行第一个非伪目标，否则仍然执行第一个目标。

自动变量

自动变量是执行规则时根据上下文动态生成的变量。

常用自动变量表如下：

1. $@

   • 含义：表示当前规则的目标文件（Target）。

   • 用途：常用于指定输出文件名。

   • 示例：

     1 2	foo.o: foo.c gcc -c foo.c -o $@

     如果目标是 foo.o，$@ 的值就是 foo.o。

2. $<

   • 含义：表示依赖列表中的第一个依赖项。

   • 用途：常用于单个依赖项的场景，例如编译 .c 文件时指定源文件。

   • 示例：

     1 2	foo.o: foo.c header.h gcc -c $< -o $@

     如果目标是 foo.o，$< 的值是 foo.c。

3. $^

   • 含义：表示依赖列表中的所有依赖项（以空格分隔）。

   • 用途：常用于需要处理多个依赖项的场景，例如链接多个对象文件。

   • 示例：

     1 2	foo: foo.o bar.o gcc -o $@ $^

     如果目标是 foo，$^ 的值是 foo.o bar.o。

CMake 系列工具使用

不同平台使用的编译工具不一定相同，有时候根据实际情况，也可能会选择性编译整个项目的一部分。如果只提供 Makefile 可能不方便。这个时候可以利用 CMake 系列工具和 CMakeLists.txt 来根据具体需求生成特定的 Makefile。

CMake 工具可以在这里下载。

检查一个项目根目录是否包含 CMakeLists.txt 以便确认它是否支持使用 CMake 系列工具。

CMake-GUI 有个 Bug，详见。

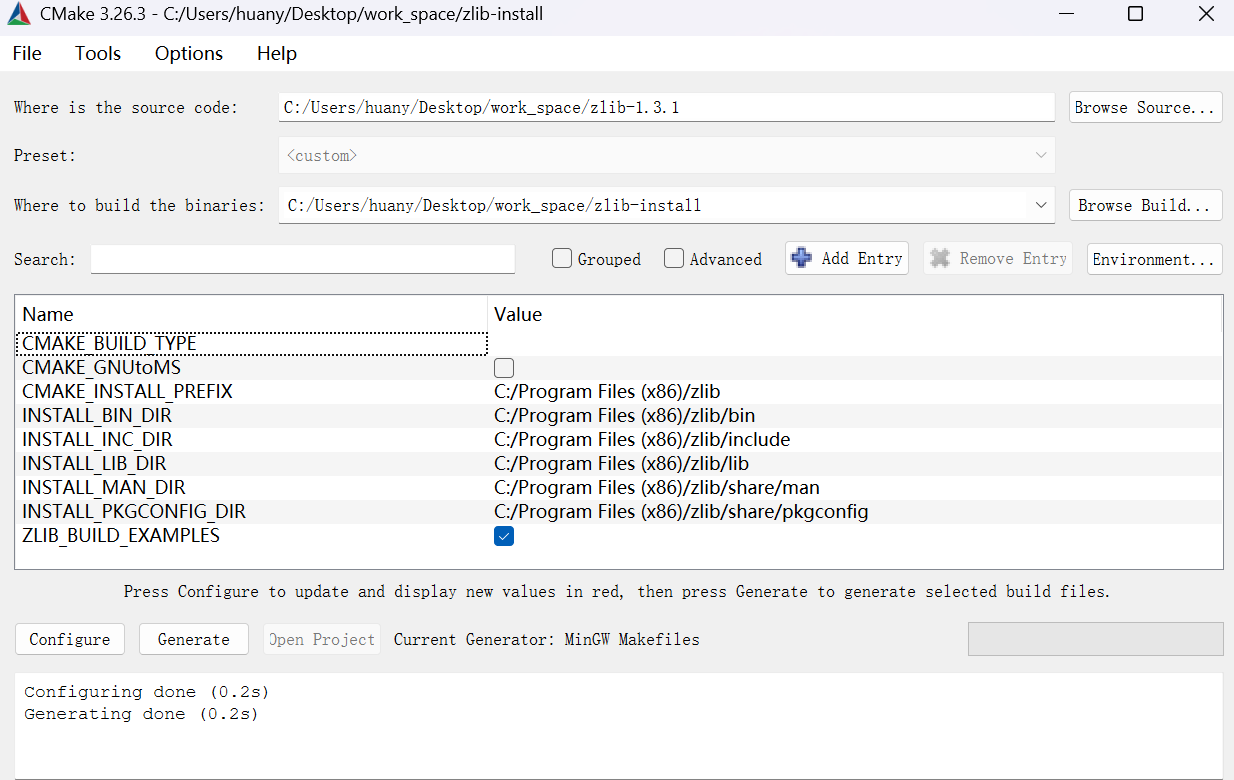
下面是 CMake 的 UI：

配置源代码和构建路径

两个位置需要填写源代码目录（包含 CMakeLists.txt）和构建目录（自己创建一个）。

Configure

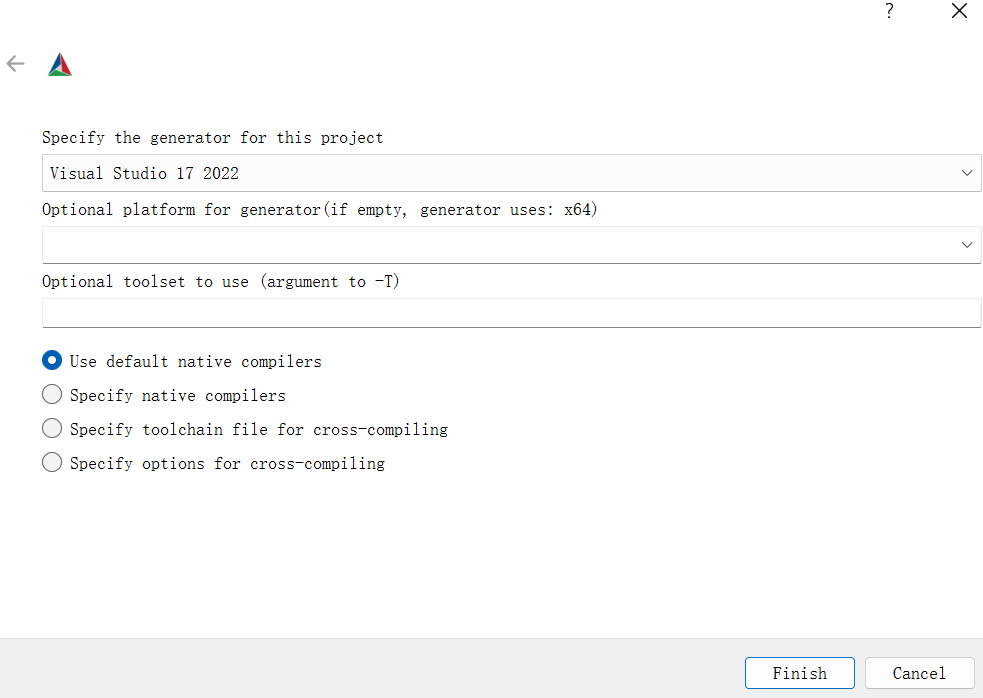
点击 Configure，会先让你选编译器之类的：

我们用 MinGW，翻一下找到选上就行，点 Finish 会自动读取所需配置项，读完之后你可以用 UI 界面方便的对它们进行改动。

Configure 过程也会读取平台信息等，大型项目 Configure 用时会很长。

如果改动了配置，需要再点一次 Configure。

由于 CMake 缓存相关的问题，如果第一次 Configure 爆红，也需要再点 Configure 一次解决问题。

Generate

完成 Configure 后，点 Generate，会在 build 目录生成 Makefile 和所需要的文件，在 build 目录执行 make 命令即可。

直接编译

gcc

命令格式：

1

gcc <功能参数> [主参数...] [包含目录参数...] [链接目录参数...] [链接参数...] [编译选项...]

1. 功能参数

   • -o：完成链接停止。
   • -c：完成汇编停止。
   • -s：完成编译停止。
   • -E：完成预处理停止。

2. 主参数

   主参数用于指定执行这次操作所需的各种文件的位置，包括 .cpp 文件、.a 文件、.o 文件等，如果这里没有显式指定，可以通过下面的参数补充指定。

3. 包含目录

   包含文件不能在主参数部分指定，必须位于包含文件搜索目录下。

   #include 除了在工作目录和系统路径搜索之外，还可以使用多个 -I path\to\include 来指定包含文件搜索目录。

4. 链接目录

   使用 -L 参数指定链接搜索目录，需要和链接参数配合使用。

5. 链接参数

   使用 -l 参数，语法规则为 -l[链接名]（注意没有空格），优先链接到链接目录下动态链接文件 /path/lib[连接名].dll 文件。如果不存在动态链接，则会链接到静态链接文件 /path/lib[链接名].a 文件。

   链接库可以在主参数中直接指定，写它的路径即可。

   例如 -L ./lib/ -lzlib 等价于主参数中添加 ./lib/libzlib.dll 或者 ./lib/libzlib.a。

6. 编译选项

   • --static：强制使用静态链接。
   • -O2：开启 O2 优化。
   • -g：生成调试符号表启用 gdb 调试功能。
   • -Wl,-rpath,<path/to/dll>：指定运行时链接搜索目录，运行时最优先到 path/to/dll 去搜索 .dll 文件，一般使用相对路径

示例（我使用了 [] 和 () 来划分部分，实际使用时需要去掉）：

1

[g++](命令) [-o main.exe](功能参数) [cli/main.cpp resource.o](主参数) [-I "C:\Users\huany\Desktop\work_space\ziptools-install\minizip-install\include" -I "C:\Users\huany\Desktop\work_space\ziptools-install\zlib-install\include"](包含目录) [-L "C:\Users\huany\Desktop\work_space\ziptools-install\minizip-install\lib\" -L "C:\Users\huany\Desktop\work_space\ziptools-install\zlib-install\lib\"](链接目录) [-lminizip -lzlibstatic](链接参数) [-fpermissive --static](编译选项)

ar

使用 ar 工具将多个 .o 文件打包成一个 .a 静态库文件。例如：

1

ar cr libmylib.a file1.o file2.o

这里，libmylib.a 是生成的静态库文件名，file1.o 和 file2.o 是输入的目标文件。

动态链接

我觉得自己造的轮子就没必要搞动态链接了，全静态吧。想起来我再补上。

软件的发布

发布 .cpp 编译生成的 .exe 软件时，需要考虑到用户的机子上没有运行环境的事实，一般采用两种方式：

• 全静态链接 --static。
• 同时发布所需的 .dll 文件，放在 .exe 同级目录下或者使用 -rpath 编译参数。
• 折中。

练习——Windows 编译 OpenCV

OpenCV 是使用最为广泛的计算机视觉库，编译文档十分完善，也有数量可观的资料可供查询。但 OpenCV 体型巨大，编译用时较长。

OpenCV源码

编译完成后应该得到以下文件：

• 包含目录 include/
• 静态链接库 lib/
• 动态链接和其它二进制文件库 bin/

练习——Windows 系统编译 minizip

minizip 是 zlib 库的一个子库，能够支持压缩和解压。minizip 目前已经放弃维护，相比成熟的 OpenCV，可能需要修改一些编译命令才能完成编译。

你需要完成 minizip 和 zlib 的编译，得到以下文件：

• zlib 的包含目录 include/ 和静态链接库 lib/。
• minizip 的包含目录 include/ 和静态链接库 lib/。

提醒：

• 注意，官方的 makefile 中可能没有生成目录的步骤，你可能需要手动创建目录或者更改 makefile。

• minizip 的 makefile 无法针对 windows 使用，请自行排查其错误并进行修改后完成编译，或者使用 g++ 手动编译生成有关文件。

• 你可以用 CMake 完成 zlib 的编译，也可以阅读下面文档手动编译：

  To compile all files and run the test program, follow the instructions given at the top of Makefile.in. In short "./configure; make test", and if that goes well, "make install" should work for most flavors of Unix. For Windows, use one of the special makefiles in win32/ or contrib/vstudio/ . For VMS, use make_vms.com.

• minizip 源代码位于 zlib/contrib/minizip/，请自行解读代码结构并进行操作。注意其依赖的 zlib 相关的配置。

大练习——编译 NcatBot 发行包

背景简介

ncatbot 旨在让用户无门槛使用，开发者只关注业务代码，提供了一个 windows 平台下的 .exe 安装部署工具。

该工具只包括一个 main.exe 主程序，能够无下载过程的配置基础 Python 环境，并安装 ncatbot 本体，调用 ncatbot-cli 完成后续交互。

相应的代码 main.cpp，Python 环境压缩包 package.zip 都已经给出，请编译出可执行文件 main.exe。

有关资源

• main.cpp
• package.zip
• zlib&&minizip

指示

main.cpp 开头部分含有编译命令，参考这一部分编译命令，你需要完成如下工作：

• 完成 zlib，minizip 的编译。
• 完成 package.zip 的编译。
• 正确书写设置 zlib，minizip 的路径和编译命令。
• 编译 main.cpp 并链接其它上述资源。

在 NcatBot-Release 中含有编译好的 zlib，minizip，package，如果你实在无法完成这些部分，可以下载使用并完成接下来的部分。

附录

命令格式书写语法

这是一种约定俗称的记号，而不是一个严格规范，每位开发者使用的书写方式不一定相同，也不会特意严格按照要求书写，下面给出我的习惯记号。

• [EXPR]：表示这一部分是可选的。
  • [mingw32-]make：可能是 mingw32-make 或者 make。
  • 有些人也会写成 ()，但一般不会写成 <>。
• <VAR>：表示一个变量，需要根据实际情况更改。
  • 有时候你会明显感觉到不用 <> 包起来也表示一个变量，自己灵活处理，例如 path/to/zlib/ 可能表示 C:/Program Files(x86)/zlib/。
  • 有时候也会写成 []。
• <VAR...>：表示这里的参数个数是动态变化的，每个参数用空格分隔，可以是 0 个。
  • <编译选项...> 可能表示 -O2 -fpermissive 或者 -O2 --static 或者 --static 或者啥都没有。
  • 有时候也会写作 [VAR...] 或者 [<VAR>...]。

更多自动变量

1. $?

   • 含义：表示依赖列表中比目标文件更新的依赖项（以空格分隔）。

   • 用途：常用于条件编译或增量构建，只处理那些真正需要更新的文件。

   • 示例：

     1 2	foo.o: foo.c header.h gcc -c $< -o $@

     如果 header.h 被修改，$? 的值是 header.h。

2. $*

   • 含义：表示目标文件的主名（不包含扩展名）。

   • 用途：常用于生成与目标文件相关的其他文件名，例如中间文件或依赖文件。

   • 示例：

     1 2 3

     %.o: %.c gcc -c $< -o $@ echo "$* is compiled"

     如果目标是 foo.o，$* 的值是 foo。

3. $+

   • 含义：表示依赖列表中的所有依赖项（以空格分隔，与 $^ 类似，但保留重复项）。

   • 用途：在某些需要保留重复依赖项的场景中使用。

   • 示例：

     1 2	foo: foo.o foo.o bar.o gcc -o $@ $+

     如果目标是 foo，$+ 的值是 foo.o foo.o bar.o。

4. $|

   • 含义：表示依赖列表中的顺序依赖项（Order-only prerequisites）。

   • 用途：用于指定那些仅用于顺序控制的依赖项，这些依赖项的更新不会触发目标的重新构建。

   • 示例：

     1 2	foo: bar.o | dir gcc -o $@ $<

     如果目标是 foo，$| 的值是 dir。

5. $(@F) 和 $(@D)

   • $(@F)：表示目标文件的文件名部分（不包含路径）。

   • $(@D)：表示目标文件的目录部分（不包含文件名）。

   • 示例：

     1 2 3 4

     build/foo.o: src/foo.c gcc -c $< -o $@ echo "File: $($(@F))" echo "Directory: $($(@D))"

     如果目标是 build/foo.o：

     • $(@F) 的值是 foo.o
     • $(@D) 的值是 build

6. $(*F) 和 $(*D)

   • $(*F)：表示 $* 的文件名部分。

   • $(*D)：表示 $* 的目录部分。

   • 示例：

     1 2 3 4

     build/foo.o: src/foo.c gcc -c $< -o $@ echo "File: $($(*F))" echo "Directory: $($(*D))"

     如果目标是 build/foo.o：

     • $(*F) 的值是 foo
     • $(*D) 的值是 build

折腾 vmware

ubuntu24.04 环境。

config apt source

打开 /etc/apt/source.list.d/ubuntu.sources，在 URIs 一项中，http://archive.ub.... 前面加上 .cn，也就是 https://cn.archive.ub....。

第二项那个 security 不用改。

vmware tools

1
2
3
4
5

sudo su
apt-get update
apt-get install open-vm-tools
apt-get install open-vm-tools-desktop
reboot

共享文件夹

开共享后, 客户机共享文件夹目录: /mnt/hgfs/

重安装的网络问题

重新安装 vmware 时，可能会遇到以下问题：

• 安装程序在 "配置网络驱动" 时卡死
• 安装后客户机死活连不上网。

这是由于卸载时没有删除注册表导致的，解决方案（参考）如下：

• 在下载的软件中翻一翻，找到 "注册表"
• 一键扫描然后修复。
• vmware 点 "编辑"，"虚拟网络编辑器"，还原默认设置。

输入法

百度输入法很靠谱，它甚至附带了安装说明。

百度输入法

先验概率 VS 后验概率

定义

• 先验概率是根据主观经验，在没有任何实验的情况下对某件事情发生概率的预测。

• 后验概率是根据某些已知证据，去估计的事情发生的概率。 \[ P(H|E) = \dfrac{P(E|H)*P(H)}{P(E)} \] 该式子中，每项含义如下：

  • \(P(H|E)\)：在证据 \(E\) 成立的前提下，假设 \(H\) 成立的概率。
  • \(P(E|H)\)：在假设 \(H\) 成立的前提下，证据 \(E\) 被观测的概率。
  • \(P(E)\)：证据 \(E\) 成立的先验概率。
  • \(P(H)\)：假设 \(H\) 成立的先验概率。

朱世衡之问

有关朱世衡提出的硬币之问，不妨设 \(E\) 表示抛 \(100\) 次硬币 \(50\) 次正面朝上，\(H\) 表示 \(p=0.9\)，也就是正面朝上的概率为 \(90\%\)。那么：

• 可以计算出 \(P(E|H)\le \epsilon\)，也就是如果 \(H\) 成立，那么观测到 \(E\) 的概率会很小。

• 不能说：因为 \(P(E|H)\le \epsilon\)，所以 \(P(H|E)\) 很小。

• \(P(E)=\int^1_0{P(p=x)\cdot P(E|p=x) dx}\)，显然 \(P(p=x)\) 是个先验概率，是确定不了的，所以 \(P(E)\) 没法计算，同理 \(P(H)\) 也没法计算，故 \(P(H|E)\) 计算不了。

最大似然

一般求解方式

• 考虑后验概率函数相对简单且为凸函数，对后验概率每个参数求偏导即可解出最大似然。
• 对后验概率函数使用梯度下降，求解极大似然。

EM 算法

算法用途

EM 算法主要用于近似求解一些最大似然问题。

算法流程

1. 初始化模型参数 \(\theta\)。
2. 对 \(\theta\) 进行迭代，优化 \(Q(\theta | \theta^{(t)}) = \mathbb{E}_{Z|Y,\theta^{(t)}} \left[ \log P(Y,Z|\theta) \right]\)。
   • 根据 \(\theta^{(t)}\) 计算 \(Z\) 不同取值的后验概率密度函数 \(F = P(Z=x|\theta^{(t)})\)。
   • 根据 \(F, \theta^{(t)}\) 求解上式的最大似然。

算法举例

有三个硬币 \(A,B,C\)，正面朝上的概率为 \(\theta_A,\theta_B, \pi\)，每次实验先抛硬币 \(C\)，如果 \(C\) 正面朝上，则使用 \(A\)，否则使用 \(B\)，一次实验抛完 \(C\) 后抛 \(A\) 或 \(B\) 五次，记录为：

1
2
3
4
5
6
7
8
9

实验一：2 正 3 反

实验二：4 正 1 反

实验三：1 正 4 反

实验四：3 正 2 反

实验五：4 正 1 反

根据实验结果给出一个最大似然参数估计 \(\theta = (\theta_A, \theta_B, \pi)\)。

E 步骤

计算每个实验由 \(A\) 或 \(B\) 生成的后验概率：
\[ \gamma_j(A) = \frac{\pi \cdot \theta_A^{n_j}(1-\theta_A)^{m_j}}{\pi \cdot \theta_A^{n_j}(1-\theta_A)^{m_j} + (1-\pi) \cdot \theta_B^{n_j}(1-\theta_B)^{m_j}} \]

M 步骤

迭代更新： \[ \pi' = \frac{\sum_{j=1}^5 \gamma_j(A)}{5} \]

\[ \theta_A' = \frac{\sum_{j=1}^5 \gamma_j(A) \cdot n_j}{\sum_{j=1}^5 \gamma_j(A) \cdot 5}, \quad \theta_B' = \frac{\sum_{j=1}^5 \gamma_j(B) \cdot n_j}{\sum_{j=1}^5 \gamma_j(B) \cdot 5} \]

迭代

设置一个收敛阈值，似然估计变化小于阈值时令其停止。

EM 原理证明

首先对似然函数取对数，记： \[ L(\theta) = \log(P(Y|\theta))=\log{\sum\limits_{z}P(YZ|\theta)}=\log(\sum\limits_{z}P(Y|Z,\theta)P(Z|\theta)) \] 考虑： \[ \begin{align} L(\theta) - L(\theta^{(i)})&= \log\big({\sum\limits_{z}P(Y|Z,\theta)P(Z|\theta)}\big) \\ &=\log\big({\sum\limits_{z}P(Z|Y, \theta^{(i)})\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y, \theta^{(i)})}}\big) - \log(P(Y|\theta^{(i)})) \end{align} \] 由 \(\text{Jensen}\) 不等式，得 \[ \begin{align} \text{上式} &\ge \sum\limits_{z}P(Z|Y,\theta^{(i)})\log{\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y, \theta^{(i)})}} - \log(P|\theta^{(i)})\\ &= \sum\limits_{z}P(Z|Y,\theta^{(i)})\log{\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y, \theta^{(i)})P(|\theta^{(i)})}}) \end{align} \] 令： \[ \begin{align} B(\theta, \theta^{(i)})&= L(\theta) + P(Z|Y,\theta^{(i)})\log{\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y, \theta^{(i)})P(Y|\theta^{(i)})}}\\ &=L(\theta)+P(Z|Y,\theta^{(i)})\log{\frac{P(YZ|\theta)}{P(YZ|\theta^{(i)})}} \end{align} \] 第二行来自贝叶斯公式。

则有 \(L(\theta)\ge B(\theta, \theta^{(i)})\)，且 \(B(\theta,\theta)=L(\theta)\)。

所以令： \[ \theta^{(i+1)} = \mathbf{argmax}_\theta B(\theta, \theta^{(i)}) \] 则有： \[ L(\theta^{(i+1)}) \ge B(\theta^{(i+1)}, \theta^{(i)}) \ge B(\theta^{(i)},\theta^{(i)})=L(\theta^{(i)}) \] 即： \[ L(\theta^{(i+1)})\ge L(\theta^{(i)}) \]

算法分析

对比

上面的三硬币问题理论上也可以直接求解最大似然，但是列出来后是一个 PDE，一般 PDE 目前是没有闭式解，所以也只能退而求其次找近似解。

梯度下降也行，但是相比于 EM，梯度下降的梯度计算比较复杂，而且无法保证满足概率约束，可解释性弱，收敛不可靠等等等。

M 步骤最大似然的求解

三个变量是独立的，分别求偏导就能代出值来。

本文介绍了 Docker 的基本操作方法, 强调了一些易错点.

本文是神经网络学习笔记，主要记录了几种常用神经网络的结构和变体，以及一些训练技巧及其原理。

本文以现代计算机网络硬件为基础，介绍了现代硬件环境下应该了解的网络知识，能够为网络编程打下一个较好的基础。

打算要写的东西

打算要做的事

NcatBot 是一个用于 QQ-Bot 开发的 Python SDK.

一些日常可能会用得上的技术（二）

写在前面

虽然很多人能够熟练掌握一门编程语言，也能用这门编程语言方便的批处理数据，但是每次总要借助这门语言的 编译器/解释器，然后调用一些系统函数之类的，总感觉缺了点意思。

Linux/Windows 其实在 shell 中已经提供了一门完备的编程语言来直接处理文件或者数据，这相比与写一份代码来运行它要有趣很多。

你不必记下本文的所有细节，只需要知道有这些所介绍的功能即可，记忆会在你的使用过程中一步步完成，AI 能提供的信息会比本文更详尽。

一些常用命令

grep

1

grep [选项] 模式 [文件...]

• 选项
  • -i：忽略大小写。
  • -r：递归搜索子目录。
• 模式
  • 默认是标准正则。
  • 用 -F 参数禁止正则（所有正则符号被视为文本）。
  • 用 -E 支持扩展正则表达式。
• 文件
  • 用 - 表示标准输入。（第一期讲过 "一切皆文件"）
  • 支持多个文件，每个文件用空格隔开。
  • 文件名可以采用通配符语法（见附录，大部分文件名参数都可以支持通配符）。
    • 通配符语法匹配的并不是相对路径，而是对于每一层目录和文件名独立匹配，也就是说 f1/*.txt 不能匹配 f1/ 子目录下的 .txt 文件。
• Windows 平替
  • 可以去下载一个 ripgrep 加入系统路径后当平替，用法基本一致，命令改为 rg。

echo

• 用于输出字符串。

  1	echo [一个字符串]

• 常用参数

  • -e：指定转义 \ 相关的换行（\n），制表符（\t）等。
  • -E：指定不转义。

• 备注：

  • 不同操作系统的 echo 标准不一样，所以有 -e-E 这种看上去反人类的参数。
  • Windows 系统的 PowerShell 也有 echo，但是它的转义符是 "`"，系统默认发生转义操作。

cat

• 题外话

  • 见下图。

    

  • 为什么学计算机的很多人都喜欢猫~~？

• 查看文件内容

  1	cat [文件...]

  • 会输出结果到终端。

• 其它用法

  • 写入文件：

    1	cat [文件...] >> file.txt

    • >：覆盖写入。
    • >>：追加写入。

  • 文件部分可以接受命令行输入，> 或者 >> 前不填写任何参数就使用命令行输入。

  • 使用 EOF

    1	cat > file.txt << EOF

    • 接下来的输入中，输入 EOF 并回车结束输入，EOF 不会被写入。

    • 如果不使用 << EOF 也不使用管道

wc

• 统计文件字数

  1	wc [文件...]

• 常用参数

  • -l：统计行数。

• 其它

  • 可以接受命令行输入。

    1	command | wc -m

head/tail

1

head [文件名...]

• 用于显示文件的最开始/最后 10 行。
• 常用参数：
  • -n：紧接着可以指定行数。
• 其它：
  • 支持命令行输入

rm

1

rm [文件名...]

• 用于删除文件。

• 常用参数：

  • -r：用于删除目录。
  • -f：忽略警告直接强制删除。

• 某个很厉害的命令：

  1

  rm -rf /

  功能是删除本操作系统下所有文件，请不要执行或者被人忽悠执行该命令！

  数据无价，谨慎操作。

zip

1

zip [选项] [压缩文件名] [被压缩文件/被压缩目录...]

• 用于创建压缩文件。
• 常用选项：
  • -r 或 --recursive：递归地包含目录，即包括指定目录及其所有子目录。
  • -u 或 --update：更新现有的 zip 文件，添加新文件或更新已存在的文件。如果不用改参数覆盖时会提示。
  • -x 或 --exclude：后面输入一些 [被压缩文件/被压缩目录...]，排除指定的文件或目录。
  • -v 或 --verbose：详细模式，显示正在处理的文件名。
  • -q 或 --quiet：安静模式，不显示任何输出。
  • -0 到 -9：设置压缩级别，从无压缩（0）到最大压缩（9）

uzip

1

unzip [压缩文件名] [参数]

• 用于解压文件，默认解压到当前目录。

• 常用参数：

  • -d：后面接一个目录，解压到这个目录，不存在会创建。
  • -l：只查看里面的文件，不解压。

• 其它用法

  • 只解压部分文件

    1	unzip [压缩文件名] [要解压的文件在压缩文件中的路径...] [参数]

管道

• 管道的一般用法是 command1 | command2 ，功能是将 command1 的标准输出作为 command2 的标准输入运行。

• 举例：

  • 使用 sort 对文件内容排序，并用 uniq 去除重复行：

    1	sort somefile.txt | uniq

  • 使用 ls 列出目录内容，grep 过滤特定模式的文件，然后 sort 排序结果：

    1	ls -l | grep "^-" | sort

变量

声明

1

key=value

• = 的左右不能用空格。
• value 加上双引号被声明为字符串，不加声明为整形变量或者浮点变量。
• PowerShell 的声明使用 $key=value。

变量引用

1
2

${变量名}
$变量名

• 第一种方式是为了防止歧义。
• 用 \ 可以转义 $。

运算

• $((expr)) 语法：

  1	$((算术表达式))

  • 举例：

    1 2 3 4

    a=5 b=3 c=$((a + b)) echo $c # 输出 8

• 自增自减：

  1

  $((a++))

• PowerShell 特性：

  1

  $a++

  • 可以直接这样使用，但是在 echo 等命令中这样做不行。

• Shell 特性：

  1	let "new_var = var1 + var2"

  • new_var 可以是一个新变量名。

总结

• 大部分时候，常用命令的正则表达式、通配符等功能就可以完成大部分需要循环和分支的操作，用得上循环和分支的地方实际上不会很多。就算真的需要用到循环这些操作，这个时候使用 Python 等脚本语言可能会更方便了。
• 好好学习正则表达式。

附录

关于一些语法

• 可变参数列表：[文件...] 是一个可变参数列表，习惯上命令行参数用空格隔开，所以它实际上表示 [文件1] 或 [文件1] [文件2] 或 [文件1] [文件2] [文件3] 等等。

关于标准正则（BRE）

• .：匹配任意单个字符（除换行符外）。
• ^：匹配每一行的开头（不占位，第一个字符仍需要被模式匹配）。
  • 也用于脱字，放在 [] 内部的最开始表示匹配除了 [] 中表达字符之外的所有字符
• $：匹配行的结尾。
• []：匹配括号内的任意字符。
• |：逻辑或操作符。
• *：匹配前面的元素0次或多次。
• +：匹配前面的元素1次或多次。
• -：行为视上下文而定。
  • 在 [] 内它是一个特殊字符，它表示一个范围，例如[a-z] 可以匹配任何小写字母。
  • 在 [] 外是一个普通字符。
• ?：匹配前面的元素0次或1次。
• {n}：精确匹配n次。
• {n,}：至少匹配n次。
• {n,m}：至少匹配n次，但不超过m次。
• \（反斜杠）：转义特殊字符或表示特殊序列的开始。
• ()（圆括号）：将多个表达式组合成一个子表达式，用于分组和捕获。

关于拓展正则（ERE）

• \b：匹配一个单词字符和非单词字符之间的边界。
• \d：等价于[0-9]。
• \D：等价于[^0-9]。
• \s：等价于[ \t\n\r\f\v]。（空白字符）
• \S：等价于[^ \t\n\r\f\v]。（非空白字符）
• \w：等价于[a-zA-Z0-9_]。（单词字符）
• \W：等价于[^a-zA-Z0-9_]。（非单词字符）
• \n：匹配换行符。
• \t：匹配制表符。
• ?：非贪婪匹配（lazy quantifier）。

关于通配符

通配符拥有部分正则的特性，支持不如正则完整，语法有微小差异，具体细节如下：

1. *：匹配任意数量的字符（包括零个字符）。
   • 例如：*.txt 匹配所有以 .txt 结尾的文件。
2. ?：匹配任意单个字符。
   • 例如：file?.txt 匹配 file1.txt、filea.txt 等。
3. [...]：匹配括号内的任意单个字符。
   • 例如：file[123].txt 匹配 file1.txt、file2.txt 和 file3.txt。
   • 也可以使用范围：file[a-z].txt 匹配 filea.txt 到 filez.txt。
4. [!...] 或 [^...]：匹配不在括号内的任意单个字符。
   • 例如：file[!123].txt 或 file[^123].txt 匹配除了 file1.txt、file2.txt 和 file3.txt 之外的所有以 .txt 结尾的文件。
5. {...}：匹配花括号内的任意选项（选项之间用逗号分隔）。
   • 例如：file.{txt,pdf} 匹配 file.txt 和 file.pdf。
6. \：用于转义自己和以上特殊符号。