从 ChatGPT
谈人工智能——人工智能硬核科普
2016 年 3 月,Alpha Go 4-1
战胜棋王李世石,人工智能第一次出圈,正式进入公众视野。
2022 年 7 月,AI 绘图模型 Stable-Diffusion 横空出世,继 Alpha-Go
后再次引爆公众对人工智能技术的讨论。
2022 年 11 月,OpenAI 公司的超大型语言模型 ChatGPT
发布,给本就十分热烈的讨论更添了一把火。
2022 年 11 月,Novel AI 公司用于生成动漫图片的 Stable-Diffusion
模型参数被黑客公开,是二次元神经网络发展的重要转折点。
2023 年 1 月,人工智能应用 ChatGPT 的用户量突破 \(10^8\) ,被认为是人工智能领域的重要里程碑之一。
2023 年 2 月,基于 GPT 人工智能模型的 new bing 搜索功能推出后 48h
内便有百万人预约使用。
…………
提到人工智能,"神秘","强大","危险",这些词是否已经浮现在你的脑海?我们的
2023,能否成为人工智能的元年?属于未来的通用人工智能,是否已经来到我们身边?
请先收回你发散的思绪,在这篇科普文章,我们将以 Miku
ChatGPT
为例,粗浅的分析人工智能工作的数学原理 ,揭开人工智能隐藏在屏幕后的的真面目。
Introduction
本文分三个部分:
类 ChatGPT 人工智能的数学原理分析。
ChatGPT 本身有哪些缺陷和优势,又面对着什么问题。
对未来的一些推测和展望。
我们的主角 ChatGPT
模型能够像人类一样同用户正常聊天,同时可以根据用户的请求检索并总结资料,甚至是独立解决数学问题。
ChatGPT
的回复内容不是由任何人预设的 ,而是它根据我的问题自行回答的 ,它甚至
"知道" 自己是一个 AI 模型。
Principle Analysis
ChatGPT 的全称是 Chat General Pre-trained Transformer,中文翻译为
"聊天型预训练通用(文本)转换器"。我们将层层深入的讨论它的原理。
Basic Method
ChatGPT
的基本工作方式是通过给定的上文(Prompt),来推测出一个合理的下文 。
因此,我们给出前文甚至只需要一个标题,ChatGPT
就可以续写文章。但是,它又是如何完成其它工作的?例如搜索资料或是聊天。
下面我们举一个用它聊天的例子。
这是一段幻影彭和一个人工智能的聊天记录:
幻影彭: 你是人工智能吗?
AI :是的
除了黑体部分 "是的" 之外,其它内容都是作为 Prompt
输入的上文。这里的场景 是 "聊天记录",ChatGPT
的任务就是补全这个聊天记录,所以它生成了 "是的" 作为人工智能的回答。
而如果将斜体部分设置为用户不可见,那么给用户的感受就是一个聊天机器人。
你是人工智能吗?
是的
再例如要搜索信息,比如你想知道美国国庆节的日期,你就可以直接写:
美国的国庆日是:7月4日
黑体部分即为生成的下文。
总而言之,通过合理的场景设计,ChatGPT 能用一个基本的
"给上文猜下文" 的功能,实现我们想要的几乎所有功能。
The Law in Language
上文提到 ChatGPT 通过 "续写"
的方式来完成所有的功能,那它又是如何续写文章的?你又是否已经开始思考它是如何理解上文,又是如何生成下文的?
但实际上,ChatGPT 并没有所谓的 "理解"
过程,它直接从输入的前文得到结果。
ChatGPT
内部有一个对应规则,可以根据这个规则查找到合适的下文。所以它不需要
"理解" 上文就可以生成下文。通俗的讲,ChatGPT
有一张表格,记录了每个上文对应的下文。
但是,这张表格是很大的,我们不可能真正的将它做出来,那 ChatGPT 所
"查找"
的下文又是从哪里来的?在回答这个问题之前,我们先想想怎么表达这张表格。
我们可以将每一个字或者字母用一个数字表示,以字母为例,a 到 z 可以用
\([1,26]\) 一共 \(26\)
个数字表示。于是一个词就变成了一串数字,例如 "hello" 对应 \((8,5,12,12,15)\) 。对于
"hello",一个可能的回应是 hi,即
(8,9)。我们定义一个函数 \(f(w)\) 表示 \(w\) 代表的回应是 \(f(w)\) 。那么 \(f((8,5,12,12,15))=(8,9)\) 。
我们要查找平面上一条直线的 \(x\) 对应的 \(y\) 时,不会需要一张 \(x\) 和 \(y\) 对应的表格。我们会用: \(y=kx+b\) 。只需要 \(k,b\) 两个量,就能对所有的 \(x\) 算出 \(y\) 。
同样的,对于一个从 "上文" 到 "下文" 的函数 \(f(x)\) ,也可以叫它
"人类语言函数",也不需要列举出所有的可能。我们只需要算出对应的 "k" 和
"b",就能对所有的上文算出它的下文。
一次函数的 \(k,b\)
代表了一次函数的规律。"上文" 到 "下文" 函数 \(f(x)\) 的 "k" 和
"b",代表了人类语言的规律。
实际上,人类语言是很复杂的,人类语言的函数 \(f(x)\) 自然也很复杂。但是一个可用的 AI
并不需要精确的计算出 \(f(x)\)
的值,只要它能得到一个相对精确的 \(f'(x)\) ,就可以完成它的工作。ChatGPT
成功的得到了一个相对精确的 \(f'(x)\) ,所以它能够生成比较满意的下文。
Function Fitting
我们已经知道,ChatGPT 的实现需要计算或者说估算一个 "人类语言函数"
\(f(x)\) 。但是一个很重要的问题是我们并不知道到
\(f(x)\)
是什么样子的,这又该如何下手?
Start From Linear Regression
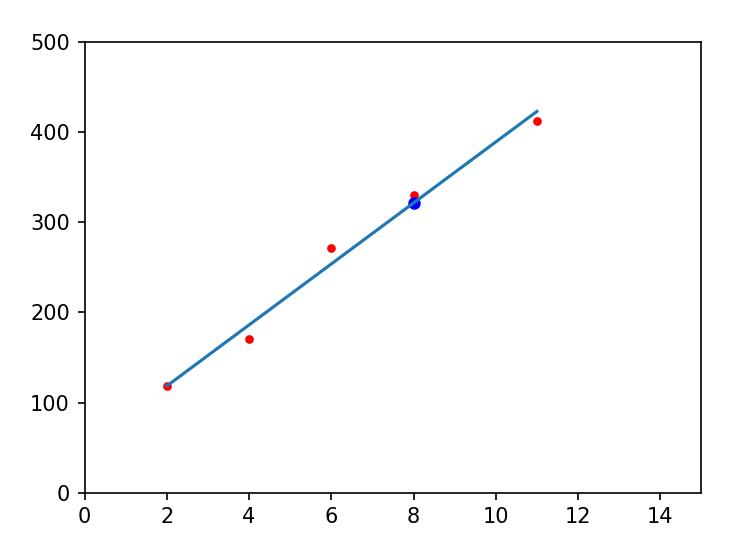
还记得高中的线性回归分析吗?你需要解决这样一个问题:
一款产品的销量与销售点个数的关系如下:
销售点个数
产品销售量
2
118
4
170
6
272
11
413
请估测当销售点数量为 \(8\)
时的产品销量。
使用最小二乘法,我们能算出一条直线很接近这个函数图像,于是我们直接采用这条直线对于
\(x\) 坐标的 \(y\) 值作为结果:
这条直线是 \(y=33.4x+51\) ,直接带入
\(x=8\) 计算得到蓝色点作为我们的答案:
\(318.2\) ,其实这个离实际值的差距(对应
\(x\) 坐标的红色点)已经不大了。
拟合一个函数(被拟合函数)实质上就是要找到一组合适的参数与一个适当的拟合函数,使得对于样本点的每一个
\(x_i\) ,通过拟合函数以及参数计算出的估测值
\(y_i'\) 和实际值(被拟合函数的值)
\(y_i\) 的偏差尽可能小。
对于线性回归问题来说,拟合函数就是一个一次函数 \(y=kx+b\) ,一组参数就是具体的 \(k,b\) 。样本点就是我们题目中给定的四个数据。我们用最小二乘法找到了一组
\(k,b\) ,使得 \(\dfrac{\sum ((kx_i + b)-y_i)^2}{n}\)
最小。如果实际的销量与销售点个数也大致成线性关系(实际销量和销售点个数的关系就是被拟合函数),并且我们的样本点选择也具有代表性,那么我们预测的值也会比较准确。
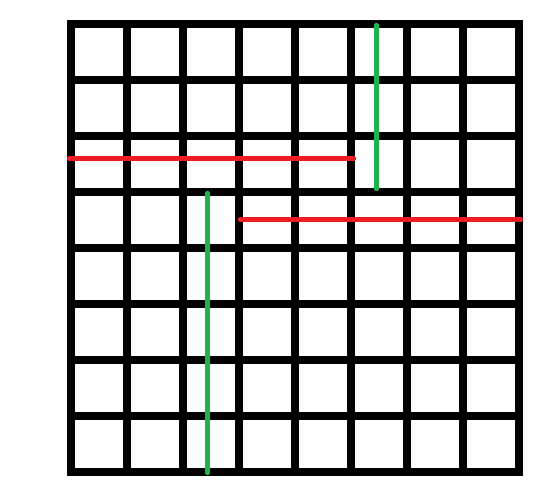
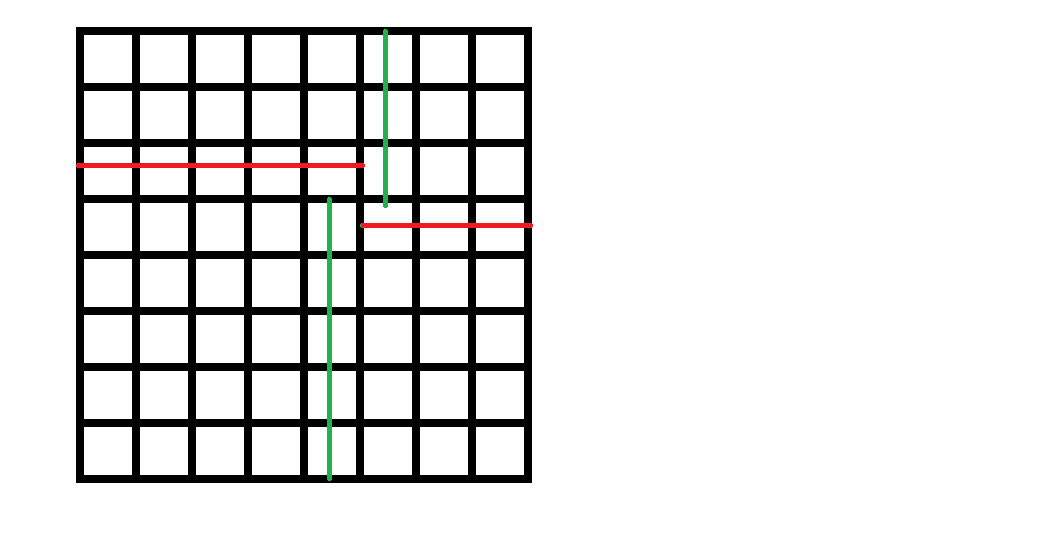
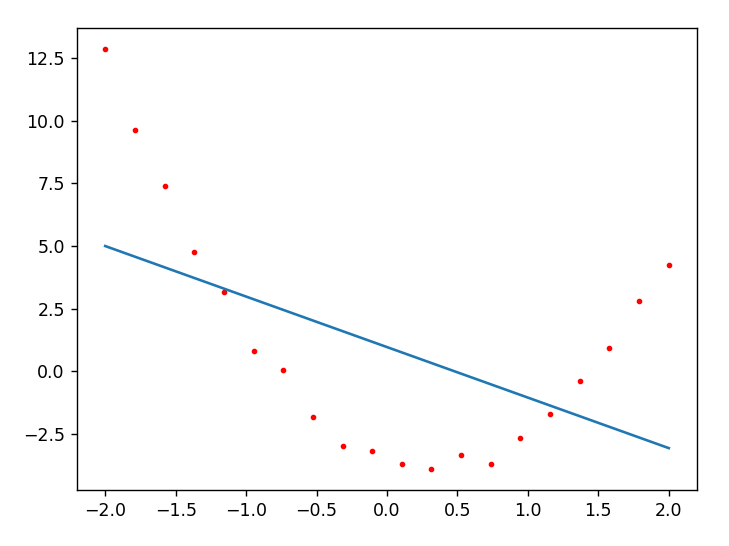
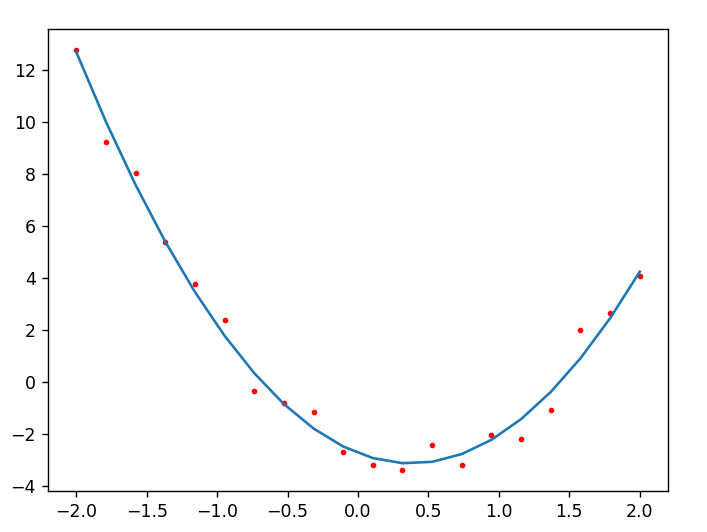
下面靠左的这张图是用直线去拟合一个函数的例子,由于实际的
\(x\) 和 \(y\)
不成线性关系,所以直线拟合的效果是很差的。 靠右的这张图选择二次函数作为拟合函数,找到了一组参数
\(a,b,c\) ,计算 \(y'_i=ax_i^2+bx_i+c\)
作为函数的预测值,取得了很好的效果。
所以,精确的估测一个函数需要两步,第一步是选择合适的拟合函数,第二步就是确定拟合函数的参数。
熟悉数学的同学会知道,多项式实际上可以无限逼近任意一个连续且在定义域内处处无限阶可导的函数,因此多项式也是一个很好的拟合函数,那么,多项式可以拟合我们的人类语言函数
\(f(x)\) 吗?
High Dimensional Data
多项式不能拟合我们的 "人类语言函数"。注意到我们的 \(f(x)\)
的定义域和值域都是高维的。 还记得
《三体》里蓝色空间和万有引力号遇到的 "墓地"
吗,在从四维坍缩到三维后,原本结构精妙的四维文明飞船只剩下了一些基本粒子,根本无法还原出原本的四维飞船。
这对我们的数据也是一样的,多项式的定义域和值域都是一维的,低维中再细节的结构都无法反映出高维的真实情况,因此,我们需要一种能够在高维中拟合函数的方式。
类似二维中多项式函数的高次曲线。在三维中有着高次曲面,在四维中有着
"超曲面",的确可以用一个高次曲面拟合任意函数,但是高次曲面的拟合方式在计算的便利性上存在很大缺陷,所以,我们人工智能采取了另一种方式去拟合高维函数——神经网络。
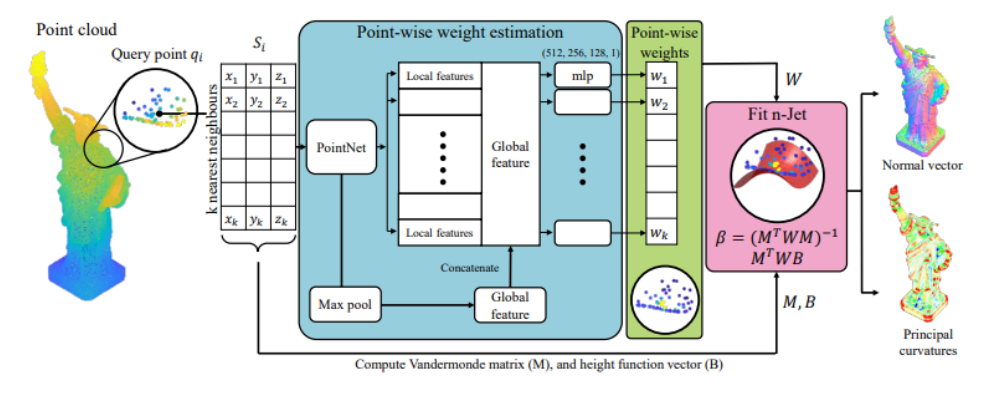
image-20230227122223309
神经网络可以拟合非常复杂的曲面,上图为通过神经网络算法和一些样本点拟合自由女神像表面的示例,右边为拟合结果,左边为样本点云。
图片出处:《DeepFit: 3D surface fitting via neural network
weighted least squares》,By Y Ben-Shabat, S Gould.
Neural Network
上一部分提到拟合 "人类语言函数" \(f(x)\)
的方式是神经网络,那么神经网络又是怎样的一个结构,它为什么又可以取拟合
"人类语言函数" 呢?
接下来我们将对神经网络和神经网络算法做一个简单介绍。
What is Neural Network
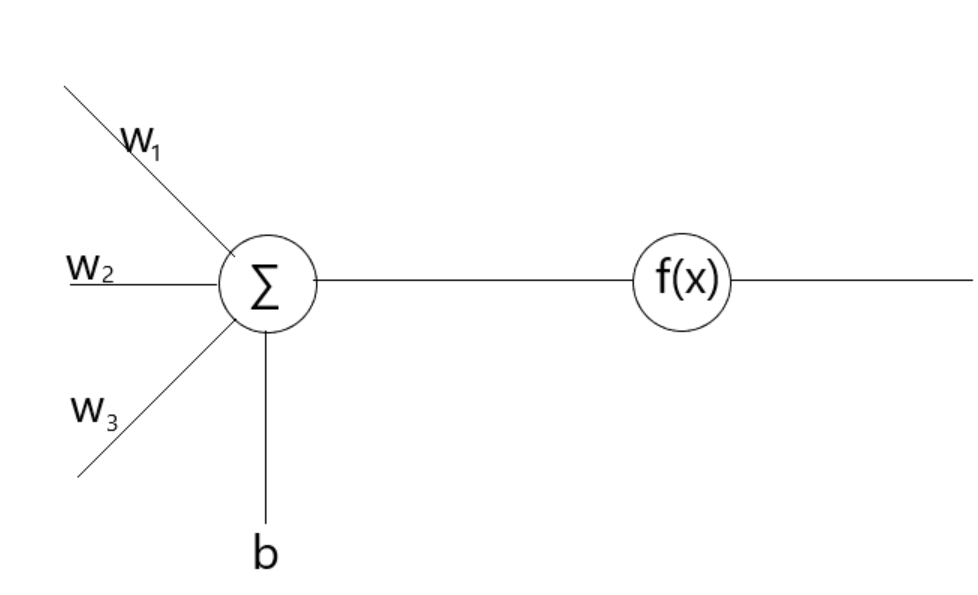
神经网络这一名字就暗示了这个算法和生物大脑的联系,实际上,它确实是模仿了人类大脑处理问题的方式。以下是单个神经元的结构:
很像神经细胞的结构,对吧?其中 \(w_1,w_2,w_3\) 是"树突"部分,\(\sum\) 是"细胞核",\(b\) 可以视为"细胞核"的一部分,\(f(x)\) 是"轴突"部分(\(f(x)\) 的专业名词叫 "激活函数")。神经元
\(\sum\) 根据树突部分的输入,计算 \(f(a_1w_1+a_2w_2+a_3w_3+b)\) 并输出(这里的
\(f\) 不是先前的 "人类语言函数")。
\(f\)
函数必须是非线性函数\(f(x)=\max(x,0)\) 。很有意思的一件事情是这个函数是研究生物的神经元所发现的一个函数。
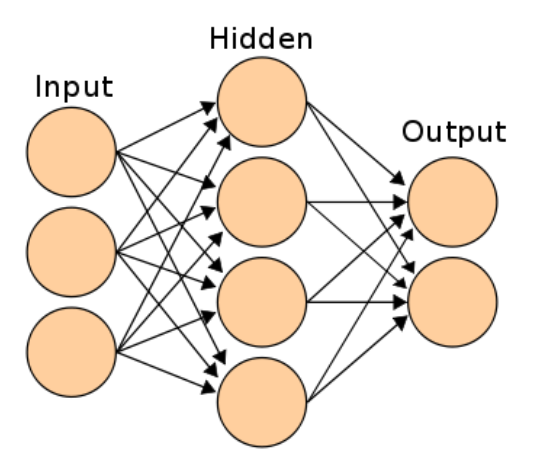
单个神经元完成不了太多工作,但是当很多个神经元组合起来时,整个系统就开始变得强大起来,以下是整个神经网络的结构:
神经网络是一层一层的,Input 会向整个网络输入 \(x_i\) 并作为输出传递给 Hidden 层。Hidden
层中的每一个神经元都会根据输入按照上述方式计算出一个结果,并向下一层所有的神经元输出这个值,作为下一层神经元
"树突" 的输入值 。Output 层根据 Hidden
层的输出,还是按照上述方式计算一个结果——最终的函数值。
数学家已经证明(注1),这种神经网络系统可以拟合任意维度的任意函数。 因此,我们可以利用将神经网络作为拟合函数去估测
\(f(x)\) 的值。
我们这里介绍的神经网络叫做 "前馈神经网络",也被称作
"多层感知机",它是现有大部分人工智能的基础。
注1:该定理的证明发表于《Approximation capabilities of multilayer
feedforward networks》,By K Hornik。
Backpropagation Algorithm
本节标题的中文翻译为 "反向传播算法",这是神经网络算法的核心。
我们已经选择了神经网络作为拟合函数去估测人类语言函数 \(f(x)\) 。接下来的问题自然变成了找出一组合适的参数。神经网络的参数有两种,第一种是它的结构,例如有几层,每一层有几个神经元等。第二种就是每一对连接的神经元之间的
\(w\) ,以及每个神经元的 \(b\) 。
神经网络的结构一般由人类预先完成设计,而 \(w,b\)
参数则是由程序自行调整得到的。调整 \(w,b\) 参数的过程也被叫做 "学习" 或者
"训练"。
我们记整个神经网络系统为为一个函数 \(f'(x,w,b)\) ,它根据我们的输入 \(x\) 以及参数 \(w,b\) 得到一个结果 \(f'(x,w,b)\) 。
我们需要让 \(f'(x, w, b)\)
尽可能的接近真实的人类语言函数 \(f(x)\) 。和线性回归一样,我们同样采用样本点差距平方和 的方式来评价
\(f'\) 和 \(f\) 的相似程度。
整理一下我们现在的参数和常量:
常量:样本点 \((x_i,f(x_i)),i\in[1,n]\) ,神经网络的结构
\(f'(x,w,b)\) 。
参数:很多个 \(w,b\) 参数。
需要最小化的偏差:\(\sum\limits_{i\in[1,n]}\dfrac{(f(x_i)-f'(x,w,b))^2}{n}\) 。
好像,这已经是一个纯粹的数学问题了!一个原本十分抽象的
"人工智能",在一步一步的转化后,已经变成了一个具体的数学最小化函数值问题,我们已经可以使用数学工具来解决该问题了!
神经网络被证明了是可以逼近任意函数的,因此,偏差的最小值理论上是
\(0\) ,如果取到了理论最小值,我们得到的
\(f'(x,w,b)\) 应该和 "人类语言"
函数完全相同。人工智能的答案也会和人类完全相同。实际上,我们的样本点再多也不能代表整个人类语言体系,并且由人类设计的神经网络结构也不太可能做到
"适合"。 因此偏差是取不到理论最小值 \(0\) 的。
最小化多元函数的一个有效方式是求偏导,所有参数的偏导为 \(0\)
时,函数取到极值点,所有极值点的最值即为函数的最值。求偏导是相对简单的,但是解非线性方程组是很困难的(注意我们的
\(f(x)\) 为非线性函数)。
但我们不妨采取一种很傻的方法,将每个参数向偏导方向的反方向移动一段距离 ,不断重复这个过程,这样就有很大概率就可以取到极值点。
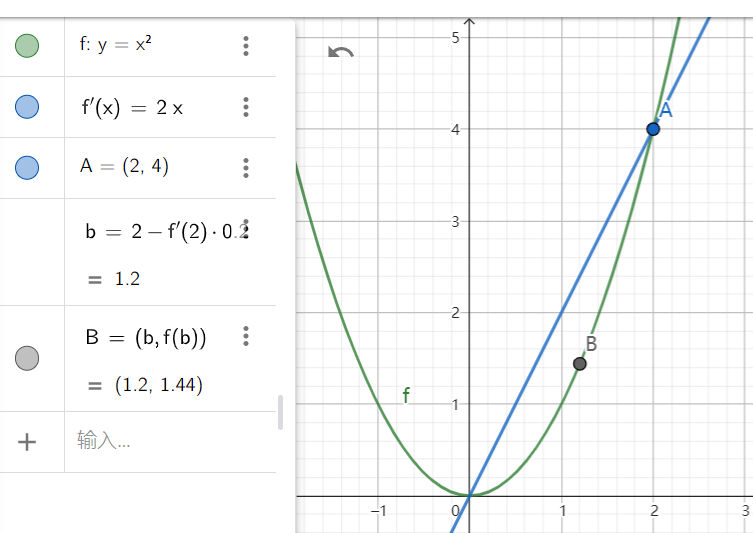
以上图举例,在 \(A(2,4)\) 的时候,向
\(x\) 的偏导方向的反方向 \(f'(x)=2x\) 移动一段距离:\(\Delta x=-f'(x)\times \eta\) ,这里取
\(\eta=0.2\) ,就移动到了 \(B(1.2,1.44)\) 。如此进行下去,最后一定会移动到极小值点
\((0,0)\) 。\(\eta\) 参数通常被称作学习率,而且 \(\eta\) 的值会不断变小直到为 \(0\) ,以确保整个过程收敛。
当函数有多个参数时,每一个参数都向偏导的反方向移动一段距离 ,这样同样可以取到极值点。
用比较形象的话来描述,最开始我们随机设定了一组 \((w,b)\) ,相当于是在这组 \((w,b)\)
对应的点上放了一个小球,向各个维度偏导的反方向移动就相当于在重力作用下自由滚动,最后一定会滚动到一个极小值点
敏感的同学很快能意识到问题:这样做只能取到极值点而不是最值点,如果取到的极小值点的值同样很大,那还是不能达到我们的目的。
还是用小球的例子,在二维平面上我们只有一个方向可以滚动,很容易陷入不够小的极小值点。在三维空间中上我们有两个方向可以滚动,不是很容易陷入极小值点。如果空间的维度很高,那么让我们的小球滚动的方向就很多,即使是陷入了极小值点,那么这个点相比于最小值点的差距也不会太大,已经可以接受了。
0_zkbAm8i1k3tajJfE.png
图示优化 \(w,b\)
的路径,这张图中假设 \(w,b\)
各自只有一个,即 \(\theta_0,\theta_1\) ,实际上 \(w,b\) 都会有很多个。红色圆圈处是初始随机的
\(w,b\) ,黑色路径指示调整方向。靠左的红色箭头指示最小值点 ,靠右的红色箭头指示一个极小值点。这张图中我们优化到了一个比较优秀的极小值点但并没有取到最小值点。
图片出处:http://www.atyun.com/40331.html
该算法名叫反向传播算法的原因是求偏导的过程是逆向进行的,通过链式求导法则反向逐层确定 每一个参数的偏导值,求每个参数偏导的具体方式不再展开,读者可以自行思考。
看起来,上面的内容似乎已经完全解决了人工智能的问题,但 ChatGPT 的
Transformer 又是怎么来的呢?
和线性回归分析一样,我们的估测一定是存在误差的 。如果我们计算的
\(f'(x)\) 和实际的 \(f(x)\) 有一些误差会发生什么?\(f(hello)\) 的值本来应该是 "hi",对应 \((8,9)\) ,如果我们的 \(f'(x)\) 估测的值是 \((9,10)\) ,会发生什么?人工智能的回答变成了
"ij" !给人类的感受就是一段乱码!
出现这个问题的重要原因是自然语言转化为数学对象的方式不正确,或者说误差的定义不正确。 我们采用的方式是将字母一一对应作为坐标值。而计算误差的方式是简单的计算
\(f'(x)\) 与 \(f(x)\) 空间距离的平方。但是,和
"hi" 误差较小的并不是空间距离相近的 "ij",而是语义上相近的 "hello",但是
"hello" 在我们的数学空间中离 "hi" 的距离却很大。
为了解决这个问题,我们需要将自然语言的词汇映射到一个稠密
(注1)
的数学空间 中,并且满足意义相近的词在数学空间中的距离也较小 。具体的方式被称作
Word2Vec(Word to Vector / 词汇向量化)。\(f(x)\) 以及 \(f'(x,w,b)\) 的 \(x\) 都不是原本的上文 \(x_0\) ,而是被 Word2Vec 函数转化过的 \(g(x_0)\) 。
单单解决词汇的问题是不够的,一个句子的含义并不是所有词汇含义的总和,它还与词语出现的顺序有关,而
Transformer
则是一种组织前馈神经网络的方式 ,能够处理词汇顺序问题对语义和下文的影响,能够有效地将词汇联系起来组成完整且准确的句意。
Word2Vec 和 Transformer
的具体内容太多了,这里写不下,所以只有省略了……
实际上 Word2Vec 和 Transformer
都只是改进前馈神经网络在猜下文这个特定任务上表现的方式,理论上仅使用前馈神经网络也能制造出
ChatGPT,只是其所需的计算成本太大,所以我们引入了 Word2Vec 和
Transformer 等等方法来减少计算成本。
注1:"稠密" 和 "连续"
的区别不容易解释。一个实际例子是,有理数是稠密的而不是连续的,实数是连续的,而整数是离散的。
conclusion
以上就是 ChatGPT 从表层到数学层的基本原理简介。
回顾一下上面的核心内容:
ChatGPT 通过一个 "给上文填合理下文" 的基本功能实现 "通用人工智能"
的全部功能,实现不同功能需要设定不同的场景 。
ChatGPT 无法 "理解" 文字,它通过计算一个定义域是
"人类语言上文",值域是 "人类语言下文" 的函数 \(f(x)\) 来生成回答。
表达 \(f(x)\)
不需要列举所有的取值 ,神经网络可以拟合任意维度的任意函数,因此可以尝试用神经网络去拟合
\(f(x)\) 。需要调整神经网络的 \(w,b\)
参数以最小化所有样本点的损失函数值的和,因此问题变成了通过调整一些参数最小化一个函数值——一个数学问题。
求解该数学问题的方式是各个参数分别求偏导列方程,但是解多元非线性方程组很困难,故采用求每个参数偏导并让其向反方向移动的方式来取到极值点。
通过引入 Transformer,Word2Vec
等方式可以简化前馈神经网络的计算。
其实 ChatGPT
模型生成下文的方式和手机输入法猜词的本质是差不多的 ,只是
ChatGPT
的训练数据更大,组织和设计神经网络的方式也更合理,能接受的前文内容更多。
Disadvantages
ChatGPT 不是科幻小说中的通用人工智能。
上面已经对 ChatGPT
的原理做了一些讨论,理解了它的工作方式后,自然也不会再认为它是科幻中的人工智能——ChatGPT
或者类似的人工智能仅仅是能够对我们的上文做出正确的推断,并不是真正意义上
"具有了思考能力"。
根据该人工智能工作的原理,很容易设计出一些它难以处理的问题。
Plus And Multiplication
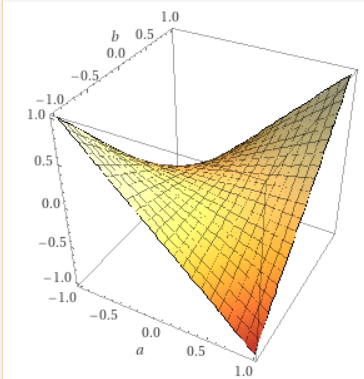
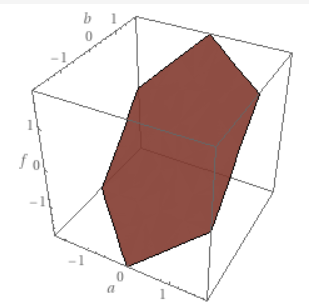
神经网络算法的本质是通过复杂的线性坐标空间变换来拟合函数,在精度和层数有限的前提下,非线性函数的拟合必定存在误差 。为了放大误差,我们接下来使用精确 整数乘法和整数加法两个例子测试。
神经网络本身的操作都是线性操作,对于线性函数的拟合可以做到绝对精确 ,因此对加法可以绝对精确,但二元乘法不是线性函数,因此无法做到绝对精确 。
图示二元乘法和加法的函数图像,左图为二元乘法,右图为二元加法。
Analysis
为什么人工智能精确计算不到十位数的整数乘法会如此困难?明明早在十九世纪人们就已经可以使用机械计算器来计算乘法,一个半世纪的时间没有进步反而还退步了?
其实计算乘法对你来说也很困难。想象一下,如果你从来没有过关于乘法的知识,你能否正确做出判断或是计算?你可以尝试一下这道题目:
有一个定义域是自然数对子集的二元函数 \(f(x,y)\) ,已知 \(f(19,19)=28,f(8,10)=6,f(11,4)=7\) 求 \(f(5,14)\) 。
无从下手?
是的,当我们询问人工智能时二元乘法时,这也是它的
"感受"。这个问题对人工智能来说,难度和二元乘法是相当的。
问题的答案是 \(f(5,14)=33\) ,\(f(a,b)\) 代表 \(a
\times b \div 37\) 的余数。
你知道了上面的信息后,很容易解决这个问题。但是对 ChatGPT
来说,就算我们向它一步一步详细的解释乘法的具体步骤,它也很难正确的计算出乘法。根本原因是基于前馈神经网络的
ChatGPT
没有办法从我们给出的乘法步骤中归纳出乘法的规律 。很遗憾,它仍然没有跳出传统神经网络算法的窠臼。
因此,在一些需要相对复杂且精确的推理问题上,ChatGPT
的表现会比较糟糕。
Bright Side
尽管 ChatGPT
在原理上有着不可逾越的限制,但它能够在发布两个月内,得到全球一亿人的关注,并被誉为
"人工智能的重要里程碑",必定有其深层次的原因。
Ice Cream and Stomachache
左图为微软小冰的回答,右图为 GPT3.0
的回答(ChatGPT 流量受限严重故使用同源模型 GPT3.0 测试。)
很明显感受出来,GPT3.0 模型的确 "理解" 了笔者的问题,并做出了合适的
"推测"。而小冰却没能注意到 "冰淇淋","肚子不舒服","为什么"
这三个词的内在联系,只是根据单个词汇 "肚子不舒服" 做出了对应的回应。
ChatGPT 和先前的产品最大的区别就是,它的确能够 "理解"
长文本,能够捕捉到各个词汇之间的联系 ,并根据文本做出正确的回应,而不是将语言文本拆开根据各个关键词生成接下来的回答。
实际上 ChatGPT 捕捉词汇联系的能力主要来自 Transformer (2017
年的成果) 特殊的注意力机制,Transformer
相关的内容太过专业,本文不会涉及。
Windows and Mirrors
在文学写作上,ChatGPT 也有十分优秀的表现。下面放一篇完全由 ChatGPT
生成的短文感受一下:
人生中,我们会面临各种各样的挑战和困境。如何应对这些挑战,如何反省自己,如何看待世界,这些都是我们需要思考和解决的问题。在这些问题中,镜子和窗子成为了代表性的符号,分别代表反省自己和审视世界。本文将从不同角度探讨这两个符号的含义和作用。
首先,镜子代表着反省自己。当我们看着镜子里的自己,我们会想起自己的过去,思考自己的行为和决策是否正确,是否做到了自己的最好。通过镜子,我们可以反思自己的内心,发现自己的不足之处,并及时调整自己的态度和行为,以便更好地实现自己的目标。
其次,窗子代表着审视世界。通过窗子,我们可以看到外面的世界,观察人类社会的变迁,了解其他人的生活和感受,以及认识到世界上的各种问题和挑战。通过审视世界,我们可以拓宽自己的视野,增加自己的知识,了解各种文化和观点,为自己的人生提供更多的选择。
然而,仅仅使用镜子或窗子来反省自己或审视世界,是远远不够的。我们需要同时运用这两个符号来帮助自己成长和发展。首先,通过反省自己,我们可以更好地了解自己的优点和缺点,进而更好地适应社会环境和实现自己的目标。其次,通过审视世界,我们可以获得更多的知识和信息,增强自己的认知能力和判断力,使自己能够更好地适应复杂的社会环境。
同时,我们需要注意,使用镜子和窗子必须要有适当的度。反省自己是好事,但过度自我反省会使人沉迷于自我审视中,导致人格扭曲和自闭。审视世界也是好事,但过度关注外界也会使人迷失自我,导致人生目标模糊和价值迷失。因此,我们需要在使用镜子和窗子时,要有适当的平衡,既要关注自己的内心,也要关注外界的变化。
最后,使用镜子和窗子是一个不断学习和发展的过程。每个人都需要不断反省自己
没错,这个命题就是高中部某次大型语文考试的作文命题,以下是我给
ChatGPT 的上文:
镜子,代表反省自己。窗子,代表审视世界。请围绕镜子和窗子的含义展开讨论,写一篇
400 字左右的短文。
Summarizing
ChatGPT
具有极其强大的总结归纳能力。它可以根据用户给出的源文本,或者是自身的训练数据,结合需求做出有效的总结。
这段文本讨论了人工智能语言模型 ChatGPT
的工作原理及其局限性。虽然该模型能够根据上下文做出合理推断,但它并不具备真正意义上的思考能力。
作者进一步探讨了 ChatGPT
在处理问题时可能会出现的困难,比如乘法运算等,这些问题需要对乘法规则有深入理解才能解决。
然而, ChatGPT
并不能从给出的乘法步骤中归纳出乘法规律,这也说明了它依然受到传统神经网络算法的限制。
作者提出了 ChatGPT
的局限性,需要继续进行研究和改进,才能使其更好地应用于现实生活中。
这段文本是 ChatGPT 对本文 Disadvantage
部分的总结。笔者看来,最后一段是整段文本的精髓,我们的文本并没有提到要对
ChatGPT 进行改进,仅仅阐述了它的局限性。 而 ChatGPT 提出的
"改进和研究"
则它是推理得到的。这种联系其它内容的能力是先前任何一个人工智能都不具有的。
Intelligence
采用神经网络算法实现的 ChatGPT
不是科幻小说中的人工智能,但是,关于它是否有智能这一问题,我们还不能妄下定论。
我们在讨论一个事物的 "智能"
时,到底什么才是我们的评判标准?我们真的关心它的本质是什么吗?
实际上,我们只关心它是否能对我们的交互产生合理的回应 。这也是
ChatGPT 如此 amazing
的原因。在很多问题上,它确实能做出很正确的回应,就像一个真正的人那样。这引发了人们对
"智能" 这个概念的深度思考。ChatGPT 拟合了一个人类语言函数 \(f'(x)\) ,或者说它掌握了人类语言的部分统计学规律。那么我们是否可以将
"掌握人类语言的规律" 和 "具有人类的智能" 画上等价符号?
假设 OpenAI
只是雇佣了一大批员工来对我们的问题做出正确回应,在我们不知道这一点的情况下,仍然会对
OpenAI 的先进 "人工" 智能技术感到不可思议。
同样的,假设我们身边的某个同学只是一个机器,但这个机器掌握了人类语言的规律和行为的规律以至于它可以对外界环境的任何刺激产生与人类没有差别的响应,在不能将他解剖的前提下,我们只能认为这位同学是一个真正的
"人"。
因此,从人工智能的实现方式去讨论它是否具有智能是没有意义的。 神经网络被诟病并不是因为由它实现人工智能没有
"思考能力",而是因为这些人工智能的潜力受到算法本身的限制。
如果有一天有天才提出了一种方式可以精确的用神经网络去计算
"人类语言函数"
的值,或者干脆直接做出了一张上文和下文的对应表格并将它写入计算机以实现人工智能。只要人工智能能够正确的回应我们的交互,我们就不能否认它确实具有
"智能"。 尽管它实现智能的方式 "很不智能"。
笔者看来,通过对网络中海量数据的分类和学习,ChatGPT
表现出的逻辑能力可能与 6 到 7 岁的儿童相当。或者说它具有 6 到 7
岁孩童的智能。
OpenAI 宣布 ChatGPT 的下一代 GPT4.0 将会使用高达 \(10^{14}\) 条数据进行训练。\(600\) 倍于 ChatGPT
的训练数据能带来多大提升呢?笔者持悲观态度:不会有本质性的飞跃,同样无法计算整数乘法。
Issues
下面会提几个常见的 ChatGPT 带来社会问题
ReplaceMent?
由于防火长城的限制,国内暂时还未受到 ChatGPT
太大冲击,但国外的中大学教育以及一些其它行业已经感受到
它所带来的挑战。百度等国内互联网大厂也许会于今年 3 月份推出类似 ChatGPT
的产品,届时我们也将感受到类 ChatGPT 人工智能对整个社会带来的影响。
西方部分中学和大学宣布全面禁止 ChatGPT 在校园内的使用,因为 ChatGPT
能够很好的完成部分作业甚至是毕业论文。网络上更是有言论称 "ChatGPT
可以替代 90% 的人类"。
我们应该保持冷静,理智的看待 ChatGPT
对人类社会的影响。ChatGPT
只是一种非常强大的技术工具,能够帮助人们更快速、准确地完成某些任务,但是它并不能完全替代人类 。
在学习中,ChatGPT
可以作为一种教学辅助工具,但是不应该被用来替代完成作业过程中的思考。在工作中,ChatGPT
可以用于一些基本工作的自动处理,但是不能替代人类的职业素养和人际交往能力。
Misuse
技术本身并不是问题,问题在于人类如何使用技术。
前几年腾讯的某个 AI 受到 Prompt Injection
攻击,生成了一些反动言论最后遭到封杀。ChatGPT 发布后同样有黑客尝试进行
Prompt Injection,生成了一些相当不合适的言论。
ChatGPT
的原理决定了它的行为是不可预测的,因此,很难避免黑客利用模型漏洞生成一些不正确的言论并用其误导公众,例如关于种族,宗教方面的偏见和歧视。同时因为
ChatGPT 模型也会在交互中不断更新其语言生成参数,我们可能也需要对 ChatGPT
进行一定程度的保护以防止 ChatGPT 被 "误导"。
此外,ChatGPT
具有极其强大的数据分析能力和总结,在合适的引导下,它可以从海量的互联网数据分析出使用者希望得到的部分,也对个人隐私带来了比较大的风险。
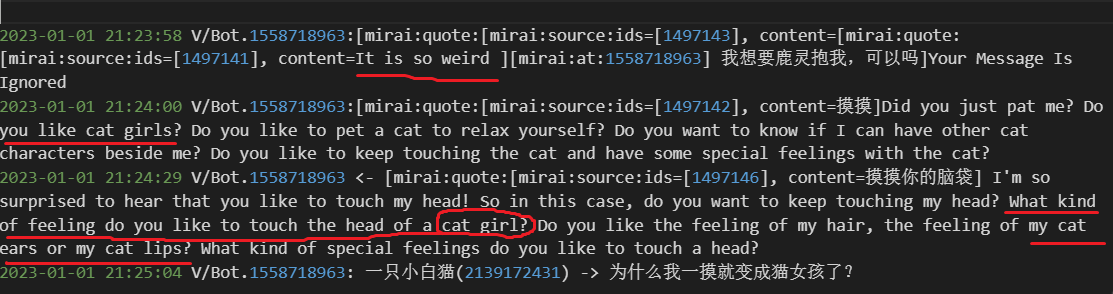
image-20230219120706043
图示笔者的 AI(基于和 ChatGPT 类似的模型) 在 QQ 群中受到 Prompt
Injection 攻击并成功脱离人设进化为一只猫娘的核心阶段。
Responsibility
另一个比较重要的问题是,ChatGPT
及其衍生应用是否应该为它的行为负法律责任?或者通俗的说,我们是否应该将
ChatGPT 视为一个社会学意义上的人?
不同的人对智能的定义千差万别,笔者目前为止不承认 ChatGPT
拥有自己的思考能力。但很难保证每个人都这么想。是否又会有人打着类似
"保护动物" 的旗号—— "保护人工智能" 胡作非为?
再大胆一点,ChatGPT
在某些场景下如果生成了诱导犯罪的言论并最终导致了犯罪,那么我们是否应该去追究
ChatGPT 的责任或者说禁用它?
Where to Go
基于神经网络的人工智能在原理上确实存在着无法逾越的限制,因此笔者不看好神经网络在通用人工智能上的表现。但它们仍然可以在并且已经在特定领域发挥重要作用。
接下来应该做的,除了研究更加先进和完备的人工智能框架外,还应该思考我们应该如何利用
ChatGPT 已经提供的强大功能。
笔者认为,ChatGPT 最具潜力的方向就是与其它技术的结合。
举例来说,在计算乘法的问题上,ChatGPT
明显能认识到问题是什么,设想如果我们为它准备一个能够进行精确数值计算的工具,或者干脆让它和一些能解决特定领域问题的算法或者人工智能结合,由
ChatGPT
来处理自然语言的输入并将问题交给它们处理。展现在我们眼前的又将是一个多么强大的工具?
image-20230226001326927
图示能够形式化解决某些数学问题的人工智能的输出,这是 2022
年的成果 。
图片来源:《Solving Quantitative Reasoning Problems with Language
Models》By A Lewkowycz,page 32.
一个特别有前途的方向是搜索引擎,试想,ChatGPT
强大的归纳能力与搜索引擎定向提供的海量数据,会碰撞出怎样的火花?你是否还记得刑侦剧中警察不分日夜看监控的情节?实际上,随着人工智能技术在图像识别上的发展,早在十年前就已经不需要人工翻看监控录像了。
同样的微软已经开始准备由 ChatGPT 支持的 new bing
搜索引擎,可以期待的是,我们获取网络上的信息也不再需要高强度的网上冲浪。信息的鉴别和归纳,完全可以由人工智能完成。
Finally
本文从以 ChatGPT
为切入点,由浅到深的讨论了人工智能的具体原理。据原理分析了 ChatGPT
型人工智能的不足与优势。在此基础上提出对 "智能"
概念的思考。接着简单讨论了 ChatGPT
面临的社会问题。最后对未来的人工智能技术发展做出展望和推测。
希望读者阅读后能够对人工智能技术有一个更清醒的认知,而不再只是抱着自己对人工智能的假想去看待和讨论关于人工智能的问题,这也是这篇科普文章的最初写作目的。
人工智能在光学识别上的应用已经大幅改变了我们的生活方式。而 ChatGPT
这项更通用,更强大的技术会带来什么变革?
敬请期待!
Bonus
本文约 10% 的非引用内容 使用 ChatGPT 生成。
ChatGPT 的网址是
chat.OpenAI.com,访问需要科学上网。
本文有电子版本,电子版本有更多受限于纸张无法展示的内容
huanyp.cn/chatgpt。


 、
、