CF1787
A
简单,不过我蠢
偶数构造显然。
奇数不存在合法方案,不用枚举。
B
简单贪心。
C
每个 \(x_i\) 的取值最多有两个,因为如果不取到边界,那么向左或者向右调整一定会变得更优。
直接做一遍动态规划即可。
D
简单图论
E
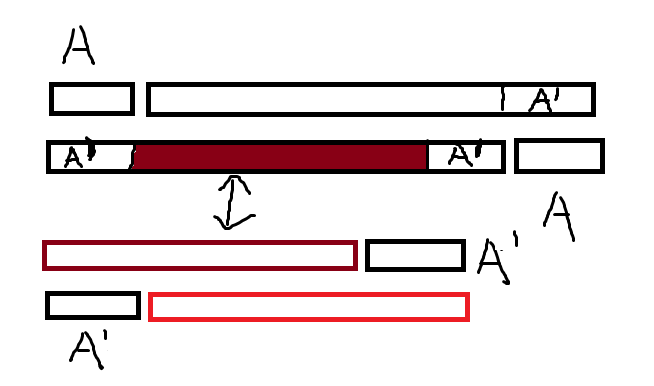
考虑能构造的一个必要条件,异或值本身需要满足且最高位的个数足够。
注意到对于连续的一段 \([1,n]\),高一位的 \(1\) 的个数不会多于低一位的 \(1\) 的个数,证明考虑最高位 (\(n\)) 和次高位 (\(n-1\)),次高位在最高位出现之前就取到了 \(2^{n-1}\),最高位为 \(1\) 时,最多有 \(2^{n-1}\) 个数取不到次高位。
对于最高位个数足够的情况,取拥有最高位的 \(k\) 个数,以及 \(a_i\oplus x\),由于异或的性质,被取到的剩下的数一定互不相同,且这样构造取到了理论最大值,将剩下的数随便塞进一组里,由于异或值本身需要满足的必要条件,一定不影响异或结果。
注意特判 \(x\oplus0\) 的情况。
F
定义排列乘法为 \(a=b\cdot c,a_i=b_{c_i}\)。
给定一个排列 \(p\) ,问是否存在一个排列 \(q\) 满足 \(q^{2^k}=p\),如果存在,构造一种循环个数最小的 \(q\),否则报告无解。
对于 \(q\) 的每个循环我们考虑乘方之后会怎样。
将一个循环 \(w\) 写出,例如 \(1,2,3,4\),自乘一遍之后变成 \(1,3;2,4\),再自乘一遍(乘最开始的排列)变为 \(1,4,3,2\)。如果以图的形式表现,\(w^p\) 表现为将第 \(i\) 个点的边连到第 \(i+p\) 个点,注意到如果 \(\gcd(p,len)\ne 1\),那么循环个数就会减小。
考虑变换后的排列 \(p\),求出其所有循环,对于奇数长度的循环,可以将它们以 \(2^i\) 的形式合并起来,这样得到的循环个数是最小的,注意 \(i>k\) 的情况。
对于偶数长度的循环,如果个数不足 \(2^k\),那么它们就无法被拼接起来,否则也只能以 \(2^k\) 为单位拼接起来。
考虑将若干个长度相同的循环还原为 \(q\) 中的循环,我们知道的是,对于 \(q\) 中的原循环,将边连向 \(2^k\bmod len\) 之后的点得到了若干个长度相同的循环,那么对于这些长度相同的循环,我们在每个循环中先取一个,然后接下来才需要取同一循环的元素。
设 \(p\) 中一个循环的长度为 \(m\),总共 \(n\) 个循环,一种简单的构造方式令 \(p\) 中第 \(i\) 个循环的第 \(j\) 个元素,占用第 \(((\frac{jk}{n})\bmod m)*n+i\) 个位置,那么显然在原来 \(q\) 的循环中,\(p\) 中每一个循环的元素到下一个元素的距离为 \(k\)。
G
考虑暴力怎么做,拿一个可重集维护所有颜色的答案,修改一个点时,暴力修改和这个点连接的所有颜色的,将它们从集合中删除或者加入。
这样做一次操作复杂度和度数有关,无法通过本题。
将问题进一步抽象后发现它并不是一个好做的问题——和 CSP-S2022T3 有点类似,这种一对多的指定整体修改问题并不好做。考虑利用问题抽象前的性质——树上问题。
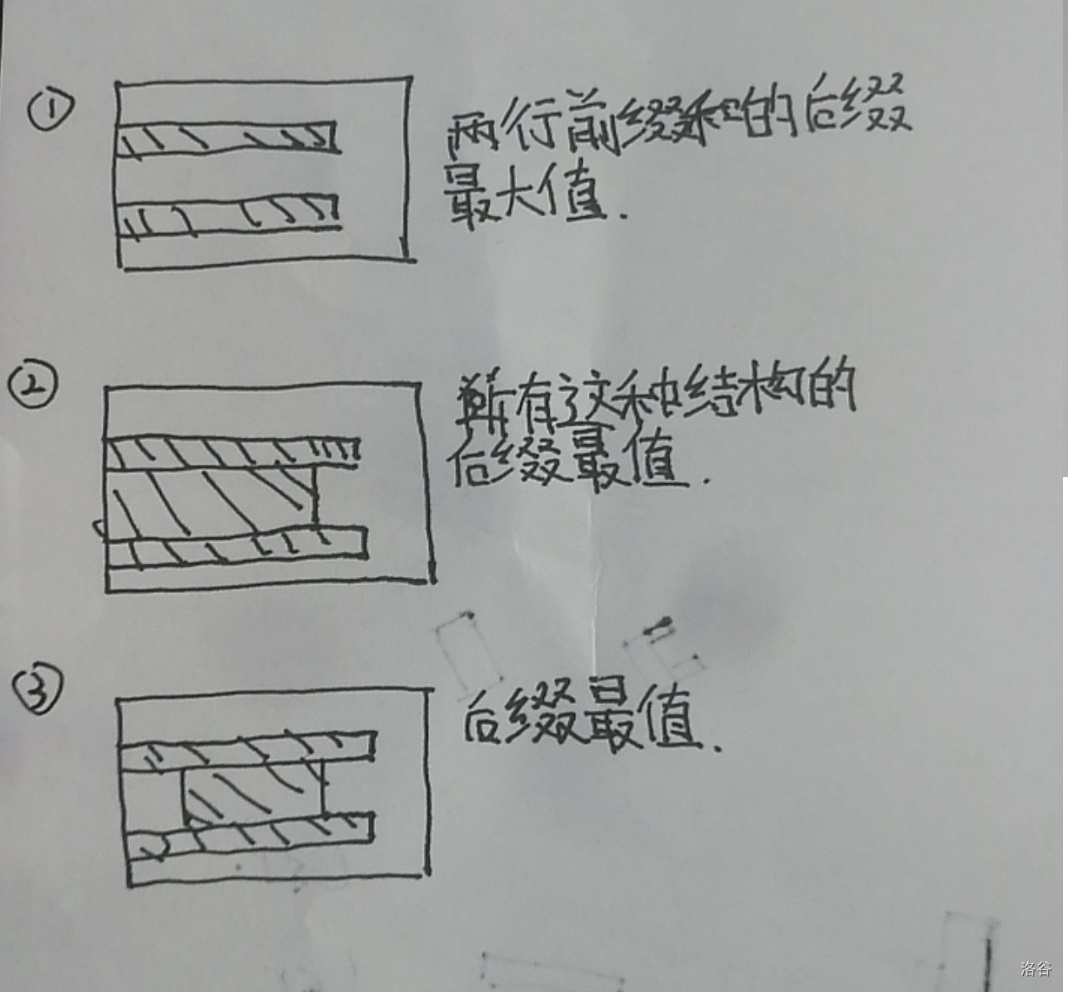
修改一个点时受到影响的颜色可以分为路径 lca 是它和不是它,后者只有一种,可以暴力修改,对于前者可以对每一个点用 priority_queue 维护路径 lca 为它的最大权值,这样就能做到 \(O(n\log n)\)。
细节有点多:
- 从树中提出链的时候,判断度数的条件应该是
(fa==0)+cnt>2则不为链,(fa==0)+cnt==1则为端点 - 不合法的颜色不应该被统计进它 lca 的 priority_queue 中。
- 如果一个 lca 不合法,那么它的权值不在总的 priority_queue 中,对它某一个儿子修改时自然不应该修改总的优先队列。