E

一个 \(n\times m\le 3\times 10^5\) 的网格，里面有一些 \(1\)，其余是 \(0\)，你需要填上尽可能少的 \(1\)，让网格上下不连通，并且 \(1\) 之间边不相邻。

这道题还是发现我网格图图论不扎实的问题。

首先很容易想到一定会存在一条自左到右的链，分隔了上下两部分。所以我直接从左到右 \(DP\)。

但是得到了 \(WA2\) 的好成绩。

左思右想也找不出问题，但是对拍后发现似乎是可以往回走的。

改成最短路算法就通过了。

矩阵图论的题目，不要只看到自左向右，要考虑存不存在往回的可能。

如果没有错过，确实很难意识到这种思维漏洞，所以一定要记住！

随便写写

昨天考试，模数很离谱 998244 8 53，我文件名还写错了，挂了 190。

考完在机房随口骂了出题人两句，自己也没当回事，题做不来，看错了，我本事不够，我认，文件名写错，我的问题。骂人，就是心情不好，也没多想。

上周有套题出的很离谱，考完也在机房骂了几句，想着反正已经考完了，相当于是下课时间，发泄几句也没什么。

上周教练下午找我聊，说要控制情绪云云，我没当回事，说 “我就是这个性格”，骂出来被批最多难受 10min，不说两句说不定憋着难受一个星期，这件事也就这么稀里糊涂的过了，高一的老师 qq 找我聊了一下，说我 "恶意发泄情绪"，我想确实是这样，虽然我还没把所谓的 "恶意发泄情绪" 当回事，不过配合老师工作，我还是接受惩罚，20 个俯卧撑当锻炼了。

昨天考完又骂了几句，然后一起考的同学都没怎么管，晚上教练叫我和我爸打个电话，打过去披头盖脸就是一顿骂，我好好的心情被这一顿搞炸了，随即想都没想就怼了回去，也没有什么目的，就是对着干，爸叫我，自己反思错误，手写检讨，晚上 11 点前拍照发给他，否则第二天来学校接我回家。

我...

说实话我确实不知道骂几句又有什么问题，搞得这么恼火，反正一下子就哭了。

稍微冷静一下去找了 Walk，和他好好聊了一会儿，其实我能想到看到的东西真的很少。。。

回想一下，Walk 说的确实有道理，再怎么说，直接骂出来是一件很不好的事情，虽然骂出来确实很爽，不过可能我不把这件事当事，很多人也不会放在心上，甚至有共情，但总有一些居心不良的人干一些龌龊的事，骂人了确实会留下一些把柄。注意，我在这里甚至用了 "居心不良" 这个非常文艺的词，而没有用一些更加常用的，更能表达我对这些人看法的词。 所以这件事终归还是我有问题。

冷静下来和老爸回个电话，说了这一点，但是爸还是说我没有看到主要问题，我这一部分看法只是很小的一面。

他说了这些点：

• 保护自己，别留下把柄（我说到的）

• 这件事让身边的其他人很难办。

• 不可避免的受到了一些网络影响。

• 情绪控制上的问题

• 文化素养的问题。

第一点就不再多谈。

第二点，这里的其它人并不指同学，指老师，他举了一个挺现实的例子，假定老师要写评语，那这件事情怎么办。可能平日里不会在意，但是比较正式和严肃的场合，爆粗口这件事情被提出来肯定会有很大的形象减分，所以为了咱还算行的个人形象，少骂几句。

第三点，我也不得不承认受到了整个 OI 圈某些不太好的风气的影响，走偏了，或者说没有守住 "本心"，在被不好的 "大多数" 带着走，以前完全没有意识到这一点，还是需要想想，是不是 "大多数"，就是正确的，这个 "大多数"，甚至还是片面的，是一个小圈子。所以，哪些是精华，哪些是糟粕，需要认真思考。

第四点，情绪控制，说起来容易，做起来难，人脑和电脑是一样的，CPU 寄存器就那几个，赛不了太多东西，情绪控制的数据都放进了内存了，但是情绪上来的时候，不要说内存延迟的 200 个周期了，L1 几个 CPU 周期你都等不了，会直接把寄存器里的情绪用最快捷的方式扔出来，放电脑上就是——"死机，爆炸"，所以最有效的方式还是多找找样本，多获取一些负反馈，让你的思维模型对情绪控制更敏感，遇到相似的输入能够把读取 "情绪控制" 模块的权重算的高一点，所以还是一个阅历的问题，样本不够，训练出来的 AI 就是典型的 "欠拟合"，处理基本问题都没有办法，换到人身上就是 "年轻人"。机器学习之所以叫机器学习那是因为它模仿了人的学习过程，是有道理的。

第五点，其实我不太想细谈，爸总是把文化素养和 "语文" 挂钩起来。我很讨厌以主观看法作为基础的一切。放在义务教育中，就是语文，历史，和政治。为什么我不把英语算进来？英语学习的是使用英语这个工具，而不是学习语文这种主观印象。除开义务教育，一个典例就是中医，也许我对中医有误解，但是至少到现在为止，我还认为它是一个以主观看法为基础的 Subject，所以直接告诉我。

考试

T1

套路状压题，有一些关于分支的常数优化技巧

T2

有趣的容斥原理题，但是不太适合出在考试。

首先猜想答案比较多，所以考场上直接一个随机化过掉。

考虑两人集合交的大小 \(\sum|S_i\bigcap S_j|\) ，如果能算出这玩意，很容易用鸽巢原理算出答案个数的下界。

考虑每个元素对它的贡献，是 \(\binom{cnt_i}{2}\) 的，所以 \(cnt\) 的分布需要尽可能平均，不妨让它就为 \(cnt_i\)。

所以上面那个式子的下界是 \(\dfrac{n^3}{4}\) 级别的。鸽巢原理，集合总个数为 \(\dfrac{n\times(n+1)}{2}\)，每一个集合先分配 \(\lfloor\frac{n-1}{2}\rfloor\) 个，剩下的数级别是 \(O(n^2)\) 的，因此答案个数是 \(O(n)\) 的，期望随机 \(n\) 次可以找到一组合法解。

T3

能看出很多问题的题。

题目本身不难，但是坑点极多。

考虑转化问题的时候一定要搞清楚转化的前提条件，以及对应的充要条件。

第一次出错：认为选定合法的删除子序列后一定有解，实际上没有位置放 \(1/0\)

第二次出错：认为必须留位置给 \(1/0\)，但实际上有可能根本不存在 \(1/0\)，留位置是没有意义的，需要特判。

另外还有必要提的一点是，这种选择一个元素，移动到任意位置的题，往往可以考虑最终结果，也就是选择了哪些，或者是选择了哪些不动。

和求改为最长不下降子序列最小代价的题目一样，可以考虑补集转化，最多的，能不动的元素个数，就是 LIS，LCS 的长度。

多次出错的原因也就是误以为只要选择合法，那么就一定可以构造合法的方案。

T4

有趣的贪心题。

我们给矿工分级，并认为操作是放一组矿工，每个矿工只能挖一个，\(k\) 级矿工能挖掉距离小于 \(k\) 的点。

考虑有一条线从下往上扫描，我们需要尽可能把矿工往上放，这样能够到更多的点。

先考虑最深的必须放矿工的点，它一定满足，\(k\) 级儿子有一个还没有被挖的宝藏，否则可以继续往上，这一定不劣，不妨从最简单的情况开始。

假设在这个点放了矿工，那矿工必须挖掉 \(k\) 级儿子，否则上面就处理不了了。如果矿工还能挖，那么需要让他把 \(k-1\) 级儿子也尽可能挖，因为如果让父亲处理，需要付出一个 \(k\) 级矿工的代价，但是这个点的矿工上到父亲的时候降级为 \(k-1\) 级，矿工等级显然越高越好，对于等级低的儿子，在这里挖可以看成于先上去降级再挖。

所以在第一个必须放矿工的点，矿工必须挖掉 \(k\) 级儿子，尽可能挖 \(k-1\) 级儿子，意思是如果还有 \(k-1\) 级儿子没有挖完，那就没必要再放矿工，可以留给父亲处理。

接下来的点就有不同等级的矿工了，对于 \(i\) 级矿工，他会尽可能挖掉和它同级的儿子，如果还有剩余，会挖掉 \(i-1\) 级儿子，这个过程一定要从等级小的矿工到等级大的矿工考虑，否则会变劣。

剩余的矿工降级后上传，儿子升级后上传。

按照这个策略贪心即可。

代码层面

由于现在考试都开 O2，所以只讨论有 O2 的情况。

循环展开

由于 CPU 处理分支的能力很烂，所以循环展开加速的一部分原因在于减少了分支。

测试标准为 \(10^5\) 次随机区间求和，大小 \(10^5\)，以下代码用时 572ms，for 循环用时 1192ms

1
2
3
4
5
6
7
8
9
10
11
12
13
14

for(int i=1;i<=m;i++){
    long long sum[4]={0,0,0,0};
    int j;
    for(j=l[i];j+3<=r[i];j+=4){
        sum[0]+=a[j+0];
        sum[1]+=a[j+1];
        sum[2]+=a[j+2];
        sum[3]+=a[j+3];
    }
    for(;j<=r[i];j++){
    	sum[0]+=a[j];
    }
    ans^=sum[0]+sum[1]+sum[2]+sum[3];
}

将 sum 数组替换为多个局部变量，效果不变。

测试了其它展开位数，开 8 位效果最佳，约 520ms。

16 位会出现寄存器溢出效率下降。

如果用的求和变量较多，最好开 4 位。

顺便一提，开 Ofast/O3 后会帮你展开。

如果你写了假的循环展开，那么效率提升只有约 \(50\%\)，这是假的循环展开，但是开了 O3 就是真的了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

long long calc(int* begin, int* end) {
	long long res = 0;
	if ((size_t)begin & 4) res = *begin++;
    unsigned long long sum[4];
	while (begin + 7 <= end) {
        auto addr = (unsigned long long*)begin;
        sum[0] += addr[0];
        sum[1] += addr[1];
        sum[2] += addr[2];
        sum[3] += addr[3];
        begin += 8;
    }
    for (int i = 0; i < 4; i++) res += (sum[i] >> 32) + unsigned(sum[i]);
    while (begin < end) res += *begin++;
    return res;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14

for(int i=1;i<=m;i++){
    long long sum=0;
    int j;
    for(j=l[i];j+3<=r[i];j+=4){
        sum+=a[j+0];
        sum+=a[j+1];
        sum+=a[j+2];
        sum+=a[j+3];
    }
    for(;j<=r[i];j++){
    	sum+=a[j];
    }
    ans^=sum;
}

用时 832ms。

减少分支

这个减少分支主要指减少内层循环的分支，尤其是理论预测成功率很低的分支。

CPU 的分支预测，可以视为一种很智能的找规律，在几乎不执行，几乎执行的情况下，或者是否成功具有循环节之类的情况，具有极高的预测效率。

当分支预测失败时，有较大可能会从内存中重新读取对应代码块，

一般可以采用乘法等算术方式。

不建议写偏向条件赋值的代码，因为高版本编译器可能会弄成条件执行，它以认为它读懂了你的代码，但是它就是个蠢逼。

在一些比较极端的情况，甚至能带来 \(5\) 倍的效率差异！

这里的 \(k=10\)。

例子：

1
2
3
4
5
6

for(int mask=0;mask<1<<(k+1);mask++){
    int final=0;
    for(j=0;j<k;j++)if(bool((1<<j)&mask))
        final^=stat[mask>>k][j];
    dp[(i+1)&1][final]+=dp[i&1][mask&((1<<k)-1)];
}

可以换成：

1
2
3
4
5

for(int mask=0;mask<1<<(k+1);mask++){
    int final=0;
    for(j=0;j<k;j++)final^=bool((1<<j)&mask)*stat[mask>>k][j];
    dp[(i+1)&1][final]+=dp[i&1][mask&((1<<k)-1)];
}

或者更理想的：

1
2
3
4
5

for(int mask=0;mask<1<<(k+1);mask++){
    int final=0;
    for(int w=mask;w;w-=w&(-w))final^=stat[mask>>k][__builtin_ctz(w)];
    dp[(i+1)&1][final]+=dp[i&1][mask&((1<<k)-1)];
}

__builtin_clz() 返回一个数二进制下前导 0 的个数，对于负数，返回值是 0

__builtin_ctz() 返回二进制末尾连续 0 的个数。

三份代码的运行时间分别为 1200ms 213ms 150ms。

高速缓存

一般情况

用一句话来说，能滚动的数组要滚动。

可以看看这两个提交，效率改进因子为 1.6。

无滚动数组，390ms。

滚动数组，150ms。

互踢缓存

如果遍历数组的顺序和数组的大小都不太理想，很容易出现互踢缓存的特殊情况，在一些极端情况可能会带来 10 倍甚至 20 倍的常数差距。

缓存存储的基本单位是 cacheline，大小为 64Byte，将一个数据物理地址的末六位抹掉，可以得到它的缓存行编号，缓存行编号视高速缓存大小和分组策略取末 \(k\) 位，作为高速缓存使用区域编号。同一高速缓存使用区一般可以存储 16 个 cacheline，如果超出，则踢出最早进入的。

举例来说，如果以 256Byte 作为步长遍历数组，那么由于抹掉 \(6\) 位后末 \(2\) 位是一样的，所以实际被利用的高速缓存仅有 \(\frac{1}{4}\)，会出现非常阴间的情况，需要避免。

访问连续

访问连续有两个层面，缓存行连续访问，页的访问连续。

一般强调前者。

算法层面

考试

A

简单题，合并两个之后一定不劣，用个栈维护还没合并的东西。

B

计数题，容易发现等价于做保证全为 \(L,R\)，此时每一行的贡献独立，考虑计算每一行单独的答案，乘上其它行的方案数，得到最后的解。

计算一行的答案，考虑每一个的贡献，好像不太行，因为你需要枚举和它配对的是什么，然后就寄了，计算的时候，我们可以决定每一个选还是不选，最后取待选的个数为 \(0\) 的所有方案，同时记录方案数和答案的和，即可完成转移。

C

有趣的题。

如果采用常规的数位DP方式，那么必须记录进位数和卡界数，只能做到 \(O(nk^4)\)。

但是不妨从结果考虑，如果能计算出恰好取到 \(n\) 的方案数，并求出 \(f(n)\)，那么答案就是 \(\sum\limits_{n\ge 0} f(n)\times 取到\ n \ 的方案数\)。考虑取到 \(n\) 的方案数怎么算。

这里定义 \(\binom{a}{b}=0 \text{ when } a<0\)。

利用容斥原理，计算强制 \(k\) 个数大于 \(x\) 的方案数。 \[ ans=\sum\limits_{n\ge 0}\sum\limits_{i=0}^{k} (-1)^{i}\binom{n+k-1-i\times(x+1)}{k-1}f(n) \] 后面那个东西，\((k-1)!\) 是个常数。

提出来后是一个关于下降幂乘上 \(f(n)\)。

把下降幂展开成关于 \(n\) 的多项式，问题变成求 \[ \sum\limits_{n\ge0} f(n)n^x \] 这个可以数位DP，考虑往后面填什么，假设已经求了 \(10^i\) 以内所有答案，往后填 \(c\)，对应的变换就是求 \(\sum\limits_{0\le n<10^i} f(10n+c)(10n+c)^x\)，把 \(c\) 扔到外面，后面哪一项用二项式定理展开，就可以用原来的值推新的值了，这东西是个卷积，但是枚举 \(c\) 的部分可以扔到外面去，预处理后是 \(O(nk^2)\) 的。

但是这是有问题的，因为我们定义的组合数和下降幂算出来的组合数是不一样的，因此需要排除掉 \(n< i\times(x+1)\) 的部分，这个可以重新数位DP一次，过程是一样的。

但是有更优雅的办法，枚举每个可能的数与 \(i\times(x+1)\) 的 LCP，然后除掉当前位后面是没有限制的，后面没有限制的答案，我们已经算过了，就是前面那个值，前面的数，已经知道了，所以合并答案的过程和刚刚没有区别，由于合并答案的过程是 \(O(k^2)\) 的，所以这样会比一般的数位DP写法更加优雅。

预处理一些东西的时候要小心，注意不要超过数组或者处理少了。

D

数据结构题。

我终归还是不会区间数颜色。

区间数颜色

需要求的东西很丑，我们的数据结构，能维护的东西是满足一些偏序关系的元素的和，但是这个东西不是这样的比较优美的形式，所以考虑转化成我们的数据结构能维护的东西。

区间数颜色，就是把不好维护的，通过一个于询问无关的 \(pre\) 数组，转化成了利于维护的偏序关系。

如果考虑区间内相同数的贡献情况，它形如 \(100000\)。

这道题可能需要求一个形如 \(\text{1 -1 0 0 0 0 0}\) 的东西。

我们发现求 \(1100000\) 也是容易的，只需要记录 pre 的 pre 就可以了。于是可以加减消元得到结果。

然后树套树。

码量极其[数据删除]。

不过直接这么搞不太行，常数太大，所以可以把每个 \(\le 10^3\) 的质因子搞出来拿个块状链表维护，再转化一下，将同一质因子视为若干线段其中 \(1-3,2-4,3-5\) 这样连，可以直接得到答案，而不用做消元。

这种把颜色连成线段的思路还是有一定的启发意义。

我实在不想写这个，下面的假莫队做法好写好调还快些。

莫队

莫队思想其实是可以做强制在线题的，这基于我们能够快速从 \([l,r]\) 拓展到 \([l,r+1]\)。如果我们能够记录当前若干个状态的值，比如 \(O(n^{\frac{2}{3}})\) 个，相当于是让每个 \(O(n^{\frac{2}{3}})\) 大小的块都能记下对应的值，然后拓展的代价就是 \(O(n^\frac{2}{3})\) 的，有些题目可能会有空间问题，得就题目讨论。

这道题一个状态需要的空间大约是 \(80000\times 4 \div 1024\div1024\approx 0.3 MB\)，可以记录约 \(3000\) 个状态，这已经够用了， \(\sqrt {3000} \approx 54\)，我们能以 \(O(\frac{nq}{54})\) 的代价回答询问，对于修改，至多影响 \(3000\) 个状态，也是可以接受的。

当然，我们需要把小于 \(1000\) 的质因子提出来单独先做一遍，以免代价过大。

但是开 \(54\) 个端点不是最优的，实践表明块长小一点，比如 \(40\) ，会更加优秀，这种分块题还是需要看实际实现来调块长。

不过 \(10^5\) 的题，怎么玩都是基本不会出问题的。

总结

时隔接近一个月写的考试总结...

考试

T1

没有什么价值的题，分析一下相位这些就可以做出来。

T2

算区间最大值之和要枚举最大值位置算跨过的数量，所以考虑对这个东西动态规划，设 \(dp[l][r]\) 表示只考虑 \(l,r\) 区间的最优答案。

枚举最大值位置后，拆分成两个区间，其答案和最大值位置以及彼此无关，符合最优子结构性质，加上最大值的额外贡献，可以在每一个位置枚举取哪个值，有可能算出来答案比较劣，但是仍然可以遍历解空间，所以这样 DP 没有问题。

枚举取值的复杂度很高，发现每个位置的最优值和 dp 数组无关，考虑预处理每个位置的最优值，本质上是给定若干一次函数，再给定若干 \(x\)，求最值，很简单。

T3

考场上没有做出来的题，但是基本想出来了，ARC 那道期望题加深了对期望的理解。

根据期望线性性，\(E(dis_{u,v} ) = E(dis_u)+E(dis_v)-2\times E(dis_{lca(u,v)})\)。

前两者是好算的，考虑这样一个 \(dp\)，\(dp_u\) 表示 \(1\) 到 \(u\) 的期望距离，转移比较简单。

考虑后者怎么算，即 \(u,v\) 两点 \(lca\) 距离的期望，如果 \(v\) 在下面，由于 \(lca\) 一定在 \(u\) 及之前，所以 \(u,v\) 的 \(lca\) 的期望等价于 \(u,u+1\) 的 \(lca\) 的期望，归纳即可证明。

考虑计算 \(u,u+1\) 的 \(lca\) 的期望值，这个也是可以动态规划的了，枚举 \(u+1\) 的祖先即可，上前缀和优化。

T4

我的想法

考虑类似点分治一样去做，只不过是随机选点，期望层数应该是 \(O(\log n)\)，证明的话，考虑将 \(\frac{n}{4}\) 个点变成一个点，分两种情况，该点存在大小超过 \(\frac{n}{2}\) 的子树和不存在。后者已经证毕，每次问题规模有 \(\frac{1}{4}\) 的概率变为原来的 \(\frac{3}{4}\)。前者考虑在该子树中选取包含根的 \(\frac{n}{4}\) 个点重复以上过程，于是不存在大小超过 \(\frac{n}{2}\) 的子树，同样证毕。

基于点分治的原理（独立的子树不跨过分治中心），可以求出每棵子树包含的点集，但如果分治的叉过多，求叉的的过程需要反复尝试每一个叉，复杂度退化到 \(n^2\)。

树形态随机的情况下（随机父亲），每个点的分叉期望是 \(\ln n\) 级别的，复杂度为 \(O(n\log^2 n)\)。

Topsort

需要问树的形态，考虑单独的一次询问能干什么，可以判断一个点是否为叶子，所以考虑从叶子一层一层往上确定。一种比较暴力的方式是先找出所有的叶子，然后删掉后找出二级叶子，找一个点当根，直接确定某个点的父亲是不好做的，考虑为某个点确定一个儿子，方式是二分，重复若干次即可。

确定一层的均摊复杂度是 \(O(leaf\log{(leaf)})\)，外加找叶子的复杂度，总计 \(O(n^2)\)，考虑优化找叶子的复杂度，一种可行的方式是先弄出一个拓扑序排列，按照拓扑序去逐一确定。

弄拓扑序可以考虑以插入的方式构造排列，一个拓扑序合法当且仅当 $  i 满足  j[1,i), p_i 不是 p_j 的祖先$。插入构造时询问一个前缀到根是否包含当前插入的点，如果包含，那么这个点应该放在更前面，得到拓扑序之后就可以逆序构造。

Subtree

考虑递归的构造，确定父亲和子树内容，假设有一个函数 \(f(x)\) 可以求出 \(x\) 子树中所有点的父亲（除自身外），那么调用每个 \(f(x)\) 一次后就可以保证求出树的结构。维护一个没调用过 \(f(x)\) 的点集，在点集中找到一个是 \(x\) 后代的点 \(y\)，调用 \(f(y)\)，于是求出了 \(y\) 后代所有节点的父亲，维护一下没确定父亲点的点集，在没调用过 \(f(x)\) 的点集中，若找不到 \(x\) 的后代，那么就可以开始在没确定父亲的点集中找出 \(x\) 的所有儿子了。

分析复杂度为 \(O(n\log n)\)。

ABC

没什么价值的题。

D

首先每次选路径一定会选到根。

要求儿子相差不超过 \(1\)。

所以每个点被选的次数弄出来了，那么每个儿子只有两种选法，选 \(\lceil\frac{cnt_u}{cson_u}\rceil,\lfloor\frac{cnt_u}{cson_u}\rfloor\)。

根据经典结论，如果直接动态规划，状态数为 \(O(n)\)。

E1

趣味题

考虑二分，发现不可二分，因为问 \(S,\overline S\) 是等价的，所以随便糊弄你就行。

所以考虑三分或者四分。

考虑解决 \(n=3\) 的基本情况。

先确定问题再处理的方式看上去不太可取。

所以我们多半是需要根据回答来决定下一个问题。

这就是一颗决策树。

问一个时，\(Y\) 的限制较强。

不妨先问 \(1\)，如果是 \(N\)，那么再问一遍 \(1\) ，还是 \(N\) 则排除 \(1\)，如果是 \(Y\) 则回到最初的 \(Case\)，此时问 \(2\)，如果回答是 \(Y\) 则排除 \(3\)，\(N\) 则排除 \(2\)。

那么用了 \(3\) 步将问题规模变为 \(\frac{2}{3}\)。

总步数为 \(3\log_\frac{3}{2}(10^5) \approx 85\)，取整之后问题不大。

F

让人眼前一亮的随机化思路。

首先可以带修莫队 \(O(n^{\frac{5}{3}})\)。但是过不了。

先考虑 \(k\) 比较小的特殊情况，不妨就是 \(k=2\)。

左想右想，都没有办法比较好的合并信息，因为它没有办法写成经典的偏序计数问题。

没有办法这样合并，那就只能 \(O(n^2)\)。

所以我不会。

这是个判定问题，只需要回答 YES NO。

考虑条件，必要条件是比较好找的，显然每个数出现次数为 \(k\) 的倍数是必要条件，若干个必要条件加在一起就是充要条件。

考虑同时判定若干个必要条件，即某些数的出现次数是否为 \(k\) 的倍数，似乎不太可做，但是发现如果随机选取若干个数并判定，那么对于答案为 NO 的所有情况，通过判定的概率至多为\(\frac{1}{2}\)，所以随机对数个子集判定后对于通过的回答 YES，正确率足以接受。

对于一个判定问题，如果有某种检测算法，答案为 YES 一定可以通过，答案为 NO 概率通过，那么运行这个算法对数次后，可以以很高的正确率回答该判定问题。

如果有一个判定问题，某随机算法能以超过 \(50\%\) 的概率给出正确的答案，那运行这个算法对数次取众数即可解决问题

A

胡乱想了一通，做出来了。

形如要求 \(f(x)=f(y)\) 的问题，可以考虑 \(f(x)-f(y)=D\)，这样就可以考察 \(x,y\) 独立对 \(D\) 的贡献了。

字典序题，从前往后贪心。

B

字典序的题，一般的方式是考虑从前往后贪心，考虑前 \(i\) 个相等的情况，并查集维护一下前面要求相等的组数，然后就是简单的组合题。

另外一种特有的方式是考虑字典序小于，和字典序大于是等价的，总方案减掉字典序相等的方案除二即可。

C

SG 函数打表，没什么技术含量。

D

很有趣的题。

二进制位相关的题目，刻画一下变换的过程，等价为在图上走。

然后发现如果 \(X_i\) 相等是好做的。

我就没啥思路了。

看一下题解。

考虑交换两个 \(X_i\) 不同的，发现最终答案不变，因为图上走的过程是等价的，继续选上之前选的边就行。

然后就做完了。

C

这里的 C 指 C2。

首先来一波 \(\pm i\) 变成相对简单的判 \(> 0\) 问题。

Method1

考试的时候，比较自然的考虑计算跨过某个数的合法区间总数，发现可以把某个位置开头最远的区间给算出来。

然后就是个二维偏序。

然后对于新修改的元素，计算跨过它的合法区间个数，如果改小了，一定只会有一些数被这个东西限制，我选择做一个极度毒瘤的二维偏序。

如果改大了，一定只会有一些数在此处的限制被放开，再处理每个数放开一次限制后的最大位置即可，对于同一位置，可以处理单点前缀和，然后在上面 lower_bound。

显然两个都是可以在线做的，但是考试的时候没有发现被限制的数一定是一个区间，然后就出现了毒瘤。

不知道自己写的什么狗屎离线做法，奇丑无比。

Method2

上面那个搞什么二维偏序是邪道。

还是考虑求跨过每个数的合法区间个数，某个位置 \(x\) 会限制另一个位置 \(i\)，当且仅当 \(a_x+i\le 0\)，所有一个位置限制的位置一定是一个前缀，这部分前缀的前缀会在这个位置之前被另外的位置限制，这是是可二分的。

所以改小的影响就好算了，找到被改小的数限制的区间，这一部分求总长度然后减去 \(cnt\times x\) 得到答案减小值。

改大会比较麻烦，参考上面的处理方式。

Conclusion

多找点性质，又不妨碍做题。

多学着点二分，别去搞什么垃圾数据结构二维偏序。

D

比较清新的构造题，难度不大，但是场上没想出来。

先假设没有操作，尝试求解该问题，发现它比较困难（似乎不存在多项式做法），所以应该考虑能不能构造出特殊情况。

考场上我看成了 reverse，这也是可做的，只需要构造出形如 0000011111 的串就行，方法是选上末尾的，插在 1 之间的 0，然后和前面的 1 交换，设 1 的个数为 \(cnt_1\)，那么选择后面 \(cnt_1\) 个位置中所有的 0，再选出前面所有的 1，交换即可。

实际上是循环左移，同样考虑构造特殊情况，这次选择构造 001100111100 这种。

如果不是，就选一个，找到下一个同样不满足的，然后移过来，最后一定有偶数个不满足的，用不同的数隔开就行。

本质上，这个操作相当于选了偶数个相邻数不同的数，把它们 flip。

平衡树

既然标题敢写平衡树，那就需要来谈谈平衡树本身，而不仅仅是实现它的方法。

平衡树本身

平衡树是一颗二叉搜索树，每个节点权值大于左子树所有节点，小于右子树所有节点。

和线段树相比，它是一种动态结构，适合维护结构动态变化的信息，比如需要支持插入和删除以及翻转的序列，也可以用来维护一棵树（LCT）

和块状链表相比，它只能处理能够快速合并的信息，但是复杂度有所降低。

实现

Splay

已经很熟悉的方式，不再多说，不过可以多嘴提一句势能分析。

势能分析原理

定义势能函数 \(F(S)\) 表示状态 \(S\) 的势能，定义操作代价 \(p_i=c_i+F(S')-F(S)\)，其中 \(c_i\) 表示操作时间。

求解 \(\sum p_i=\sum c_i + F(S_m)-F(S_0)\)

移项得到 \(\sum c_i=\sum p_i+F(S_0)-F(S_m)\)

一般来说，\(c_i\) 会比较奇怪，但是通过 \(F\) 函数的变化值可以去抵消掉这个奇怪的值得到优雅的 \(p_i\)，然后一般来说最后的复杂度和 \(\sum p_i,F(S)\) 同阶

分析 Splay 的复杂度和单旋的复杂度

定义势能函数，定义单点势能 \(w(u)=\log_2(size_u)\)， \(F(S)=\sum\limits_{u\in S} w(u)=O(n\log n)\)。

旋转点为 \(x\)，父亲为 \(f\)，祖父为 \(g\)。

左旋代价

注意到 \(size_{x'}=size_{fa}\)。

\(1+w(x')+w(fa')-w(x)-w(fa)\le 1+w(fa)-w(x)\le 1+w(x')-w(x)\)

双左旋代价

\(1+w(x')+w(f')+w(g')-w(x)-w(f)-w(g)\le 1+w(f')+w(g')-w(x)-w(f)\)

\(w(f)\ge w(x),w(f')\le w(x')\)

\(w(x')-w(x)\ge w(f')-w(f)\)

\(1+w(f')+w(g')-w(x)-w(f) \le 1+ w(x')+w(g')-2w(x)\)

若 \(w(x')-w(x) \ge 1\)

则 $ 1+ w(x')+w(g')-2w(x)(w(x')-w(x))$

否则因为先旋的 \(f\)，所以 \(g'\) 下的点不包括 \(x\) 中的点，所以有 \(size_x\ge size_{g'}\)，因此 \(w(x')-w(g') \ge1\)

得到 \(1+ w(x')+w(g')-2w(x)\le 2(w(x')-w(x))\)

综上 \(1+w(x')+w(f')+w(g')-w(x)-w(f)-w(g)\le 3(w(x')-w(x))\)

左右旋代价

\(1+w(x')+w(f')+w(g')\le 1+w(f')+w(g')-w(x)-w(f)\le 1+w(f')+w(g')-2w(x)\)

由于最终 \(f',g'\) 都是 \(x'\) 的儿子，所以 \(1+w(f')+w(g')-2w(x)\le2w(x')-2w(x)\)

所以 \(1+w(x')+w(f')+w(g')\le 2w(x')-2w(x)\)

双旋代价

注意到只会进行一次 zig 操作，所以可以忽视 zig 的那个 1，其余代价直接相加，得到 \(3\)，因此 \(p_i=O(\log n)\)。

观察到一次 Splay 操作的每个子操作可以弄成 \(3\) ，然后相加抵消掉得到 \(3+3w(x')-3w(x)\)，是 \(O(n\log n)\) 级别，势能变化量为 \(O(n\log n)\) 级别，故时间为 \(O(n\log n)\) 级别。

单旋代价

单旋代价为左旋代价的和，每次 Splay 操作数为 \(O(n)\)，故单旋的复杂度上界是 \(O(n^2)\)

总结

以上势能分析对 Splay 操作的要求是非常严格的，因此如果在查询中没有进行 Splay 操作，那么操作时间无法导致对应的势能变化，最后出现不正确的复杂度。

Treap

数据随机的情况下，一个堆（每个节点的权值均大于它全部后代的权值）的期望高度是 \(\log n\) 的，通过左右旋保证堆的性质，可以保证 Treap 的复杂度，左旋右旋和 Splay 完全相同。

FHQ_Treap

元素 val：需要维护的值。

权值 height：随机的，用于保持堆性质的值。

核心操作是 Merge 和 Split。

过程中需要时刻保证满足堆的性质

merge(u,v)

合并两个子树 u,v ，保证 u 中元素全部小于 v，返回根。

和线段树合并非常像。

1
2
3
4
5
6
7
8
9
10
11

int merge(int u,int v){
    if(!u||!v)return u^v;
    if(height[u]>height[v]){
        son[u][1]=merge(son[u][1],v);
        push_up(u);return u;
    }
    else{
        son[v][0]=merge(u,son[v][0]);
        push_up(v);return v;
    }
}

Split(u,x,y,k)

按照元素值小于等于 \(k\) 划分为两颗树，较小的那棵树树根为 \(x\)，较大的那个树根为 \(y\)。

细看这个函数其实相当妙。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

void split(int u,int &x,int &y,int k){
	if(u==0){
    	x=y=0;
        return ;
    }
    if(val<=k){
        x=u;
        split(son[u][1],son[u][1],y,k);
    }
    else{
		y=u;
        split(son[u][0],x,son[u][0],k)
    }
    push_up(u);
}

其实也可以按照子树大小划分，用于文艺平衡树。

其它操作

• get_l(element)：按照小于 element 划分，然后返回较小那边的大小，重新 merge
• get_element(rank)：与 splay 没有差异。
• insert(element)：按照小于等于它划分，然后 merge 两遍。
• erase(element)：按照小于等于它划分，然后按小于它划分，然后把划分得到的两个儿子 Merge 起来再 merge，然后再 merge，这样是能够处理元素相同节点的。
• get_prev(element)：按照小于它划分，用 get_element()
• get_next(element)：按照小于等于它划分，用 get_element()
• 合并的时候也可以按概率选择父亲，\(sz\) 较大的权重较大，期望复杂度可以证明是 \(O(n\log n)\) 的。

某些实验

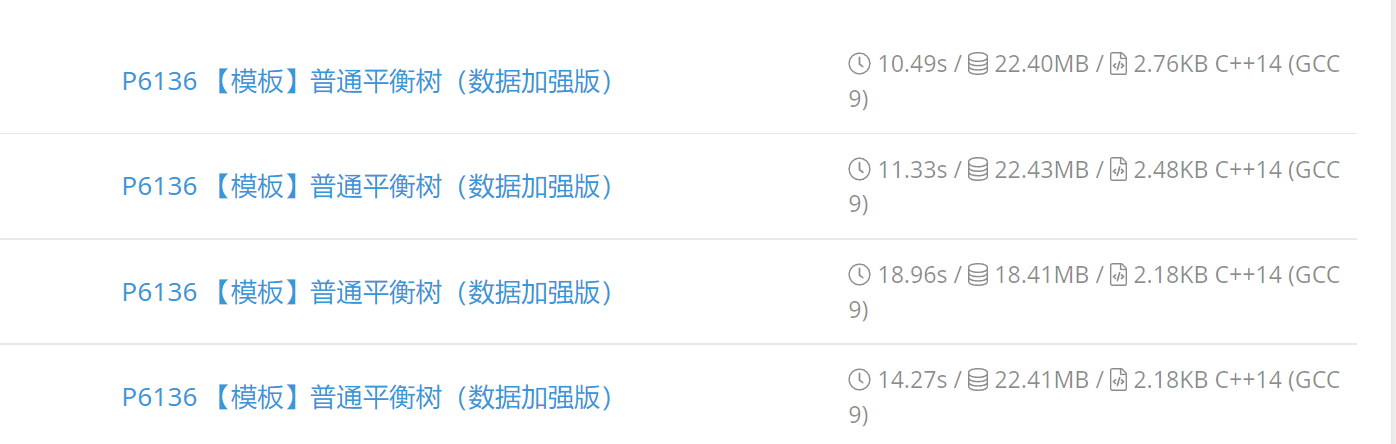
采用佳老师的神奇插入删除方式：

可以发现正常的插入方式需要 \(14S\)，\(18S\) 是按子树大小概率合并，加上佳老师优化后变为 \(10S\)，有一定改进。

如果直接实现 get_rank 系列函数可以更快，但是没什么必要了。

手写 get_rank 系列后耗时为 \(9S\)，手写 get_rank 系列，采用正常插入方式，用时 \(12S\)。

全实现的 Splay 需要 11S。

vector

一般来说，如果数据范围 \(\le 5\times 10^4\)，或者时限比较宽松，可以用 vector 实现平衡树。

pb_ds

自带平衡树，一般用于操作比较简单的情况，如果需要打 Tag 之类的，重写 node_update 不如手写一颗。

可持久化平衡树

可持久化平衡树一般用于解决强制在线的历史版本问题，对于非强制在线问题，其实可以离线到树上实现一个支持撤销的平衡树。

对于强制在线问题，基本思路都是复制修改过的路径，复用没有修改过的路径。

可以发现其实任何一个版本创建之后就是静态的，所以可持久化数据结构的核心是：任何时刻访问先前的版本，都能得到正确的结果，任何修改不能影响到先前的版本。

Splay 实现

其它操作不变，Splay 时复制涉及的所有点作为一个新版本。

但是，这玩意的复杂度有问题，Splay 的复杂度保证在于对操作进行势能分析，引入可持久化后，势能的变化量会变成 \(n^2\log n\) ,因此复杂度会退化。

由于实际应用中，很少存在只能用 Splay 的情况，因此没有必要深究 Splay 的可持久化。

FHQ-Treap 实现

听说这种实现有点问题，但是实际中并没有出现过问题，如果觉得不太行可以换下面那种奇怪的实现。

Split

由于操作都是从 Split 开始的，所以每次 Split 前都复制一个版本出来，具体的，像可持久化线段树一样把不变的儿子共用，改变的儿子复制。

Split 的路径上所有点的信息都被改变了，需要复制一遍得到新的，这样原先版本的所有节点不会有任何变化。

大致刻画以下 Split 中被修改的点，它呈一条链

Merge

Merge 过程中的复制不是必须的，原因是每个被修改的点都是被新建出来的点，这个证明可以考虑归纳，合并深度为 \(1\) 的节点时，两点显然都是被复制的，不影响原树，合并任何被复制的两个节点时，较小的那个的右儿子，较大的那个的左儿子要么不存在，要么是被复制的，因为在被复制的节点处，链一定会向下延申。

因此合并时可以不用新建节点。

神奇方法

佳老师有一个神奇写法，理论常数为 \(\frac{1}{2}\)，具体的，插入和删除时先找到第一个 key 小于当前点 key 的点，然后这个点一定是被插入/删除点的儿子，然后把只对这个儿子做一遍 Split，并把树分到插入点的两个儿子上面去，这个思路同样可以用于一般 FHQ-Treap，运用在普通平衡树中，实际效率改进因子在 \(0.33\) 左右。

一般来说删除就正常搞，不然容易写错。

考试的时候如果不卡常就写正常写法，减少可能的错误。

一般来说，空间得开 50 倍。

注：效率改进因子，若效率改进因子为 \(x\)，原时间 \(t\)，则改进后时间为 \(\frac{t}{1+x}\)。

Treap 实现

由于期望树高是 \(\log n\) 的，所以直接复制所有已经被修改的点的信息

某种奇怪的实现

类似 FHQ-Treap，但是 Merge 的时候按照子树大小作为权重，随机选一个做父亲，这样的复杂度是有保证的。

文艺平衡树

文艺平衡树是一类用于维护区间的平衡树，它和正常的平衡树类似，但是用树的结构来决定一个元素的大小，适合用来维护结构动态变化的序列。

一般用 Splay 和 FHQ-Treap 实现。

FHQ-Treap 实现时需要支持按 size 划分。

动态树

一般用 Splay 实现，复杂度 \(O(n\log n)\)，进行实链剖分，每条实链被一颗 Splay 维护，思想和文艺平衡树类似，用平衡树树的结构表明了原树节点中的的高度关系。

核心操作是 access 和 make_root。

access(x)

使得 \(x\) 到树根上的路径成为一条实链，断开 \(x\) 和它实儿子的连接，并让 \(x\) 成为该 Splay 的根。

make_root(x)

使得 \(x\) 成为树根，操作方式是先 accsess，然后翻转这条实链，使得 \(x\) 的深度最小。

由于虚儿子认父不认子，所以整个结构都没有问题。

实现

一般采用 Splay，FHQ-Treap 也没有问题。

但是不能用一般 Treap，因为一般 Treap 对树结构的要求决定了它无法进行旋转操作。

FHQ-Treap 的复杂度很难证明是 \(n\log n\)，但是可以保证上界为 \(O(n\log n^2)\)，Splay 的复杂度则为 \(O(n\log n)\)

似乎有 \(O(n\log n)\) 的 FHQ-Treap 实现。